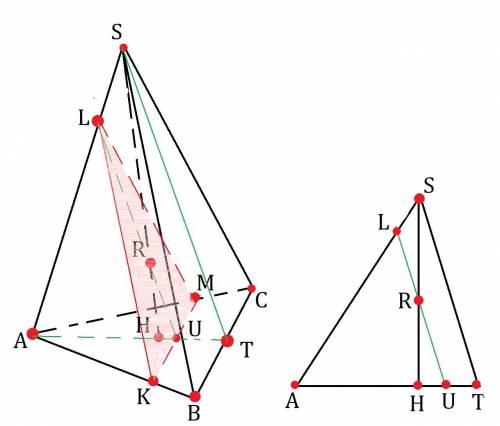
a) K, L, M ∈ α; α║(SBC)
KL║BS; KM║BC; ML║CS как линии пересечения двух параллельных плоскостей с одной общей.
SH⊥(ABC); AT⊥BC; H∈AT как центр правильного треугольника лежащий на медиане. AH:HT=2:1 по свойству пересечения медиан.
LU⊥KM ⇒ KU=UM ⇒ U∈AT ⇒ LU⊂(AST) ⇒ LU∩SH
Рассмотрим плоскость AST.
LU║ST как линии пересечения двух параллельных плоскостей с (AST).
AK:KB=AL:LS=5:1 по теореме о пропорциональных отрезках.
AU:UT=AL:LS по теореме о пропорциональных отрезках.
Как уже известно AH:HT=2:1. Пусть AU=5x; UT=x ⇒AT=6x ⇒ AH=4x; HT=2x ⇒ HU=2x-x=x.
ΔSHT~ΔRHU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит SH:RH=HT:HU=2:1. Пусть SH=2y; RH=y ⇒ SR=2y-y=y ⇒ SR=y=RH
То есть плоскость делит высоту пополам.
б) AT=AB*sin 60°=(15+3)*√3/2=9√3.
ΔAST~ΔALU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит AL:AS=LU:ST=6:5.
HT=1/3 *9√3=3√3 т.к. AH:HT=2:1
SH=13 ⇒ ST=√(169+27)=14 ⇒ LU=5/6 *14=35/3.
ΔAKM~ΔABC по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит KM:BC=AK:AB=5:6 ⇒ KM=5/6 *18=15.
Как было указано в начале LU⊥KM ⇒ S=1/2* 15*35/3=175/2=87,5
ответ: 87,5.
Дано:
АС=7 см;
АВ=25 см;
ВС=24 см.
СО – высота, проведенная к АВ.
Высота, пересекаясь со стороной, к которой проведена, образует прямой угол.
То есть угол ВОС=90° и угол АОС=90°.
Следовательно ∆ВОС – прямоугольный с прямым углом ВОС и ∆АОС – прямоугольный с прямым углом АОС.
Пусть АО=х, тогда ВО=АВ–АО=25–х.
По теореме Пифагора в прямоугольном треугольнике ВОС:
ВС²=ВО²+СО²
СО²=ВС²–ВО²
СО²=24²–(25–х)²
СО²=576–625+50х–х²)
СО²=–х²+50х–49 (Ур 2)
По теореме Пифагора в прямоугольном треугольнике АОС:
АС²=АО²+СО²
СО²=АС²–АО²
СО²=7²–х²
СО²=49–х² (Ур 2)
Тогда можем составить уравнение, объединив Ур 1 и Ур 2, получим:
–х²+50х–49=49–х²
50х=98
х=1,96
Тоесть АО=1,96 см.
Подставим значение АО и известное значение АС в уравнение СО²=АС²–АО², получим:
СО²=49–3,8416
СО²=45,1584
СО=6,72 см.
ответ: 6,72 см.