168 кв ед
Объяснение:
1)Рассмотрим прямоугольный треугольник АВН(<Н=90°)
<В=90°-45°=45° => треугольник АВН - равнобедренный. АН=ВН=24
Площадь прямоугольного треугольника равна половине произведения его катетов :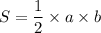
а=АН=24, b=ВН=24
тогда площадь треугольника АВН равна:
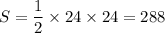
2)Рассмотрим прямоугольный треугольник CВН(<Н=90°)
По теореме Пифагора найдём катет СН:
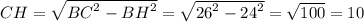
Площадь треугольника СВН(катет а=СН=10, катет b=ВН=24):
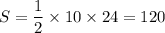
Площадь треугольника ABC равна разности площадей треугольников АВН и СВН:
S(ABC)=S(ABH)-S(CBH)=288-120=168 кв ед.
x²+ (y –65/18)² = 29/1
Объяснение:
Центр окружности имеет координаты О (0;уо) .
Точки, принадлежащие окружности имеют координаты (4;0) и (0;9). Их координаты удовлетворяют уравнению окружности:
x²+ (y – у₀)² = R² , где (0;у₀)-координаты центра .
х²+(0- у₀)²=R² , или 16 +у₀²=R²
х²+ (y- у₀)²=0²+(9- у₀)² или 81-18у₀+ у₀²= R² Вычтем из 1 уравнения 2. Получим :
16-81+18 у₀=0
18 у₀=65
у₀=3,6. Центр имеет координаты О (0; 3,6).
Найдем R²=(4²+(0-3,6)² )= 29. R=5,4
x² + (y – 21,7)² =29
Рассмотрим прямоугольный треугольник с катетами 20 и 21. Его гипотенуза и будет диагональю прямоугольника. По теореме Пифагора,