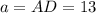Периметр прямоугольник равен 12 см, а длины его сторон относятся как 1: 2 , вычислите радиус окружности описанной около этого прямоугольника

👇

Ответ:

Пандochka

11.07.2022

Ш=2, д=4,Диагональ прямоугольника--это гипотенуза треугольника и диаметр окружности. Находим гипотенузу по теореме пифагора и делим на 2. Получится радиус. 2²+4²=20 √20=4.47 4.47÷2=2.23 R=2.23см

4,4(82 оценок)

Открыть все ответы

Ответ:

jarinka2804

11.07.2022

Дана правильная четырёхугольная пирамида SABC

.
б) Если сторона основания a=AD=13

м,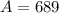

см² - площадь полной поверхности.
Из всего что мы можем найти сразу это периметр основания:
Так как по условию пирамида правильная, то в основании лежит квадрат, тогда периметр основания вычисляется следующим образом:
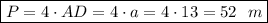$\boxed{P=4\cdot AD=4\cdot a = 4\cdot 13 = 52\,\,\,\, m}$ - периметр основания
Из формулы нахождения площади полной поверхности найдем площадь боковой поверхности:
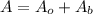A=A_o+A_b

, где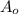

- площадь основания.
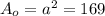Площадь основания в данном случае: A_o=a^2=169

м²

тогда площадь боковой поверхности:
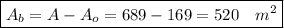
$\boxed{A_b=A-A_o=689-169=520\,\,\,\,\,\,m^2}$

Рассмотрим грань SDC

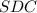, площадь этой грани будет 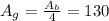$A_g= \frac{A_b}{4} =130$ м² (разделили на 4, потому что граней 4, а мы ищем площадь одной грани). Исходя из этого, мы можем найти апофему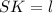 SK=l

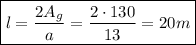$\boxed{l= \frac{2A_g}{a} = \frac{2\cdot130}{13} =20 m}$ - апофема.

г) Если задано P=44

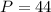м,

м²
В основе лежит квадрат, найдем сторону основания пирамиды:
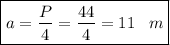$\boxed{a= \frac{P}{4}= \frac{44}{4} =11\,\,\,\,\, m}$ - сторона основания.
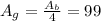Площадь грани: $A_g= \frac{A_b}{4} =99$ м², исходя из этого, найдем апофему правильной пирамиды
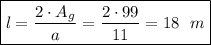$\boxed{l= \frac{2\cdot A_g}{a} = \frac{2\cdot99}{11} =18\,\, \,\, m}$ - апофема.

Площадь полной поверхности:
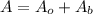
A=A_o+A_b

Вычислим площадь основания правильной четыр. пирамиды
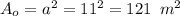
$A_o=a^2=11^2=121\,\,\, m^2$

Непосредственно вычислим площадь полной поверхности:
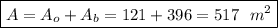
$\boxed{A=A_o+A_b=121+396=517\,\,\,\, m^2}$
Дана правельная четырехугольная пирамида. обозначим: а - сторона основания, l - апофема, p - перимет

Дана правельная четырехугольная пирамида. обозначим: а - сторона основания, l - апофема, p - перимет

4,6(7 оценок)

Ответ:

влад2162

11.07.2022

Теорема 1

Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то прямые параллельны

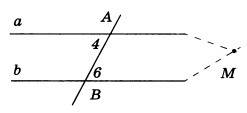
Доказательство.(с накрест лежащими прямыми)
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.