На рисунке обозначены:
ABC - Основание пирамиды
OS - Высота
KS - Апофема
OK - радиус окружности, вписанной в основание
AO - радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO - двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)
Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).
Свойства правильной треугольной пирамиды:
боковые ребра правильной пирамиды равны
все боковые грани правильной пирамиды являются равнобедренными треугольниками
в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (пи делить на 3 или 60 градусов ).
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан
1-ая задача:
вкратце)
расстояние- это перпендикуляр
поэтому треугольник АВН прямоугольный.(Н- точка расстояния от М до АВ)
угол САМ равен МАН(т.к. АМ бисс)
АМ- общая сторона
из этого АСМ=АМН(треугольники)
из чего СМ=МН=7см
ответ:7см
2-ая задача:
Любая точка биссектрисы неразвёрнутого угла равноудалена от сторон этого угла.
Доказательство:
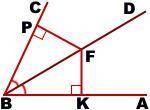
Рассмотрим треугольники BFK и BFP.
∠BKF=∠BPF=90º, ∠KBF=∠PBF (так как по условию BD — биссектриса ∠ABC).
BF — общая сторона.
Значит, ∆BFK=∆BFP (по гипотенузе и острому углу).
Из равенства треугольников следует равенство соответствующих сторон: FK=FP.
Что и требовалось доказать.

Далее рассматриваем тр.-ник ECD.В нём EC=CD(следовательно треугольник равнобедренный) и проведён диаметр EK.Нам нужно доказать,что он (EK) перпендикулярен CD.Для этого строим FC и FD,опять равнобедренный треугольник FCD,где FC=FD.Из равенства углов ECD=CDE и FCD=FDC получаем,что ECK=KDE.Выходит,что треугольник ECF и EDF равны по двум сторонам и двум углам между ними.Из этого следует,что угол CEK=DEK.
Теперь вернёмся к треугольнику ECD.В нём EK-биссектрисса,а значит и медиана.Отсюда следует,что CK=KD.Теорема доказана.