Сумма внешних углов любого выпуклого n-угольника равна 360° Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. Внешний и внутренний углы составляют развернутый угол, их сумма равна 180°. Тогда внутренний угол равен для правильных:
треугольника – 180°-(360°:3)=60°
четырёхугольника – 180°-(360°:4)=90°
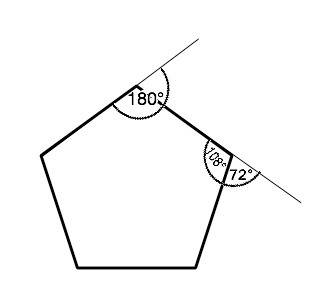
пятиугольника – 180°-(360°:5)=108°
шестиугольника – 180°-(360°:6)=120°
десятиугольника – 180°-(360°:10)=144°
восемнадцатиугольника 180°-(360°:18)=160°
S=1/2 a*b
sin 30°=a/c=1/2
c=2a
a²+b²=c²
a²+b²=(2a)²
a²+b²=4a²
b²=3a²
b=√3a
S=1/2a*b=1/2a*√3*a=√3/2* a²
S=√3/2*a²=5783√3
a²=5783√3/√3*2=11566
a=√11566
катет преднадлежащий этому углу b
b=√3a=√34698