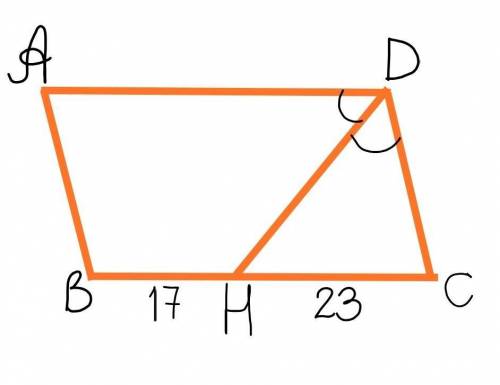
Так как противоположные стороны параллелограмма параллельны, то угол СНD=угол ADH как накрест-лежащие при параллельных прямых AD u BC и секущей DH.
Биссектриса делит угол на два равных угла.
Следовательно угол СDH=угол ADH.
Исходя из найденного: Угол СHD=угол CDH.
Тогда ∆CHD – равнобедренный с основанием HD.
У равнобедренного треугольника боковые стороны равны, тоесть CD=CH=23 см
Противоположные стороны параллелограмма попарно равны.
Следовательно: AD=BC=BH+HC=17+23=40 см; AB=CD=23 см.
Периметр параллелограмма – это сумма длин всех его сторон.
Тоесть Р=AD+AB+BC+CD=40+23+40+23=126 см.
ответ: 126 см.
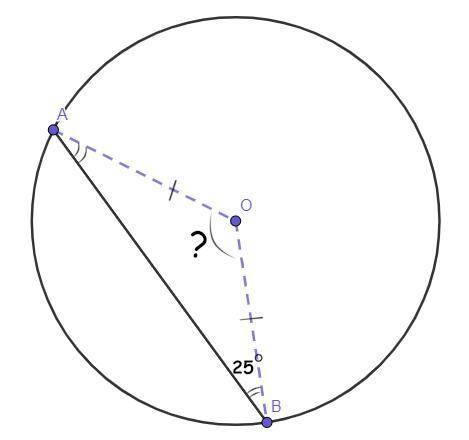
АВ хорда окружности с центром в точке О. Найдите угол АОВ, если угол АВО = 25°.
- - -
Дано :Окружность.
Точка О - центр данной окружности.
Отрезок АВ - хорда окружности.
∠АВО = 25°.
Найти :∠АОВ = ?
Решение :Рассмотрим ΔАВО.
Отрезки АО = ВО (так радиусы одной окружности), следовательно, ΔАВО - равнобедренный (по определению).
У равнобедренного треугольника углы у основания равны.Основание ΔАВО - отрезок АВ (так как АО и ВО - боковые стороны).
Тогда -
∠АВО = ∠ОАВ = 25°.
Сумма внутренних углов треугольника равна 180°.То есть -
∠АВО + ∠ОАВ + ∠АОВ = 180°
∠АОВ = 180° - ∠АВО - ∠ОАВ
∠АОВ = 180° - 25° - 25°
∠АОВ = 130°.
ответ :130°.
====================================================