Прямая касается двух окружностей, точки касания удалены от центров на радиусы. Так как радиусы равны, точки касания равноудалены от центров и лежат на прямой, параллельной линии центров.
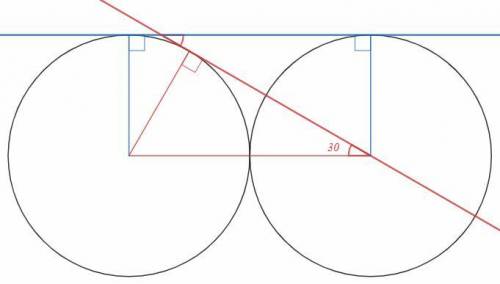
Окружности касаются внешним образом, точка касания лежит на линии центров, расстояние между центрами равно двум радиусам. Радиус, поведенный в точку касания, перпендикулярен касательной и образует прямоугольный треугольник, в котором линия центров - гипотенуза. Катет равен половине гипотенузы, значит он лежит против угла 30.
Искомый угол является накрест лежащим при параллельных и равен 30.
1) Проводим отезок, перпендикулярный каждой из параллельных прямых
2)Делим его попалам-точка О-центр окружности; ОМ-радиус; М-на одной из паралл. прямых)
3) Через О проводим прямую, параллельную данным прямым
4)Проводим окружность с центром в точке А и радиусом ОМ
5)Точка пересечения этой окр-сти с прямой из 3)! и будет центром искомой окружности