ответ: Расстояние между центрами окружностей = 12
Объяснение: Смотрите рисунок.
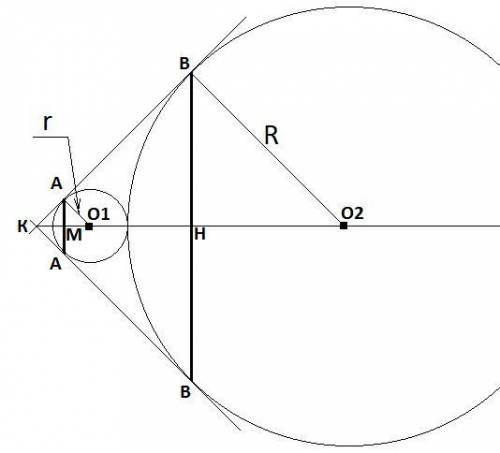
К – точка пересечения касательных. Угол К – прямой. КО2 – биссектриса угла К. А и А, а так же В и В – точки касания окружностей касательных. АА и ВВ – хорды окружностей, пересекают биссектрису в точках М и Н соответственно. О1 и О2 – центры окружностей. На рисунке видно, что расстояние между центрами окружностей О1О2 = r + R. Найдем r. АО1 параллельна КА. Т.к КО1 – биссектриса угла К, то АА перпендикулярна КО1. Следовательно ∠КАМ = ∠МАО1 = 90/2 = 45° Т.к. ∠АМО1 = 90°, то ∠АО1М = 180 – 90 – 45 = 45°. Таким образом, ΔАМО1 – равнобедренный и О1М = АМ = (2√2)/2 = √2. Следовательно, r = √{(√2)² + (√2)²} = √4 = 2. Аналогично для R: О2Н = ВН = (10√2)/2 = 5√2. Тогда R = √{(5√2)² +(5√2)²} = √(25*2) + (25*2) = √100 = 10. Расстояние между центрами окружностей = 2 + 10 = 12

То, что медианы пересекаются в одной точке и делятся точкой пересечения в отношении 2/1, считая от вершины, доказывается самостоятельно, и это можно использовать.
Дальше, если у двух треугольников общая высота и равные стороны, к которым эта высота проведена, то их площади равны. Поэтому из 6 треугольников попарно имеют равные площади те треугольники, у которых стороны вместе образуют сторону исходного треугольника.
Формально это выглядит так.
Треугольник ABC, A1 - середина BC, B1 - середина AC, C1 - середина AB, медианы AA1, BB1, CC1 пересекаются в точке G. Можно записать, что у нас есть два треугольника площадью S1 (прилегающих к стороне AB - AC1M и BC1M имеют общую высоту - расстояние от M до AB, и равные стороны AC1 и BC1) , два - площадью S2 (BA1M и CA1M), и два площадью S3 (AB1M и CB1M);
Так же равны площади треугольников ABB1 и CBB1 (точно так же - AB1 = B1C, высота общая, расстояние от B до AC). Отсюда
2*S1 + S3 = 2*S2 + S3;
то есть S1 = S2;
Точно так же из равенства площадей ACC1 и BCC1
2*S3 + S1 = 2*S2 + S1;
S3 = S2;
всё доказано.
Равенство площадей можно увидеть "непосредственно". К примеру, расстояние от точки M до BC в 3 раза меньше расстояния от точки A до BC. Это легко показать, если провести соответствующие перпендикуляры и вспомнить, что MA1/AA1 = 1/3; из подобия треугольников такое же отношение будет и у высот треугольников ABC и AMC. У этих треугольников общая сторона AC, а высота AMC к этой стороне в 3 раза меньше, значит, и площадь в 3 раза меньше.
А медиана MA1 делит AMC еще на два равных по площади треугольника - у них общая вершина напротив равных сторон, то есть общая высота к равным сторонам. Это всё.