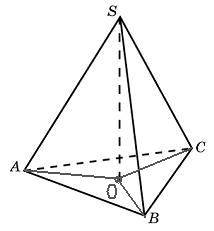
Шар описан около пирамиды, значит основание пирамиды вписано в круг - сечение шара, Н - центр основания и центр сечения, НС - радиус сечения.
Радиус окружности, описанной около правильного треугольника:
r = a√3/3, где а - сторона треугольника.
CH = AB√3/3 = 9√3 / 3 = 3√3 см.
Центр шара - точка О - лежит на пересечении высоты пирамиды и серединного перпендикуляра к ее ребру.
SO = OC = R - радиус шара.
OH = SH - SO = 10 - R
ΔOHC: ∠OHC = 90°, по теореме Пифагора
CO² = OH²+ CH²
R² = (10 - R)² + 27
R² = 100 - 20R + R² + 27
20R = 127
R = 6,35 см
Первая наклонная АС с проекцией ОС и перпендикуляром из А к плоскости образует равнобедренный прямоугольный треугольник АОС, где ОС=АО.
Этот треугольник - половина квадрата с диагональю АС.
По свойству диагонали квадрата
АС=10√2 см
Длина наклонной АВ вдвое больше расстояния от точки А до плоскости, т.к. это расстояние противолежит углу 30°
АВ=2·10=20 см
АД, образующую с плоскостью угол 60°, можно найти по теореме Пифагора.
ОД равно половине АД, как противолежащая углу ОАД=30°.
АД=2ОД
АД²=ОА²+ОД²
4ОД²=100+ОД²
3ОД²=100
ОД=10:√3
АД=20√3
А можно найти АД из формулы высоты равностороннего треугольника ( Ведь АОД - половина такого треугольника). Результат будет таким же.
Так как трапеция равносторонняя, то AB=CD=(8+18=26), тогда:
AB+CD=26+26=52.
P=AB+CD+AD+BC=29(AB+CD)=2*52=104.