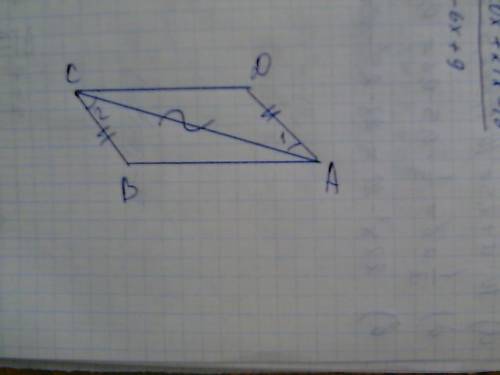
Как известно, диагонали точкой пересечения делятся пополам, а противоаоложные стороны пар-мма равны. Следовательно, противоположные по отношению друг к другу треугольники равны(по 3-ему признаку равенства треугольников), и площади их тоже равны.
Осталось доказать, что площади двух "смежных" треугольников равны. Рассмотрим их. Одна сторона у них общая, примем за основание сторону, лежащую на диагонали. Эти стороны у треугольников равны, т.к. точкой пересечения, повторюсь, диагонали делятся пополам. Прощадь треугольника у нас равна половине основания, умноженного на высоту, проведенную к основанию. Проведи к основаниям треугольников высоту - это будет один и тот же отрезок.
Мы получили - основания у треугольников равны, высоты равны.
Теорема доказана.
а) R = 4см.
б) при расположении точки М на малой дуге ВС, <BMC = 150°, при расположении точки М на большой дуге ВС, <BMC = 30°.
Объяснение:
а). Так как трапеция вписана, она является равнобокой, => АВ=СD=4см, <A = <D = 60°.
Так как угол А=60°, то угол ВDА=30° (сумма острых углов прямоугольного треугольника равна 90°). Против угла 30° лежит катет, равный половине гипотенузы (свойство). AD = AB*2 = 4*2=8 см.
Так как вписанный угол АВD равен 90°, то AD - диаметр описанной окружности.
АD = 2R = 8см, следовательно радиус равен AD/2 = 4 см.
ответ: R = 4см.
б). Угол ВМС - вписанный по определению, следовательно, он равен половине градусной меры дуги ВС, на которую опирается.
Если точка М расположена на большей дуге окружности, стягиваемой хордой АВ, то он равен градусной мере вписанного угла BDC, опирающегося на эту дугу, то есть 30° (<D - <BDA).
Если точка М расположена на меньшей дуге окружности, стягиваемой хордой АВ, то он равен половине градусной меры дуги BАDC, то есть (360°-60°)/2 = 150°.
ответ: при расположении точки М на малой дуге ВС, <BMC = 150°, при расположении точки М на большой дуге ВС, <BMC = 30°.