Нам известны все 3 измерения прямоугольного параллелепипеда, значит мы можем найти его диагональ.
a, b, c - его различные рёбра; d - его диагональ.
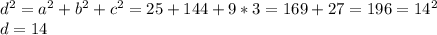
ответ: 14 см.
Если 3√3 выражен в см.
Доказательство этой формулы:
Все грани прямоугольного параллелепипеда прямоугольники, это определение. Поэтому квадрат диагонали основания будет равен a²+b². Рассмотрим плоскость в которой есть диагональ параллелепипеда и наша диагональ прямоугольника из основания. Это плоскость образует сечение, которое является прямоугольником т.к. боковые рёбра перпендикулярны основанию, а наша диагональ прямоугольника лежит именно в основании. Так вот одна сторона прямоугольника это боковое ребро, а вторая это диагональ, которую мы искали вначале. При этом диагональ этого прямоугольника и является диагональю параллелепипеда, то есть d²=c²+(a²+b²), т.к. это прямоугольник. Что и требовалось доказать.
Смотри на рисунок, для понятности.

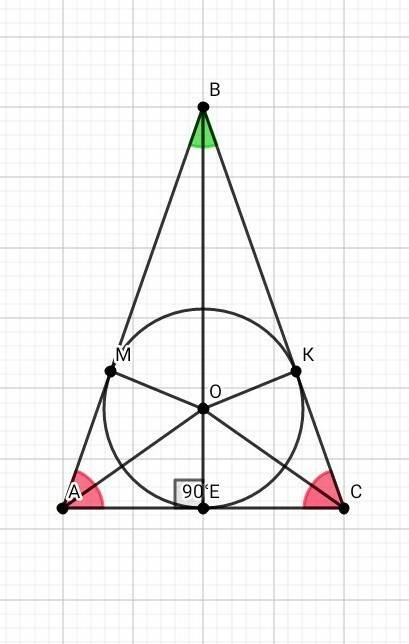
основание высоты из С на АВ Н, из В на АС - К.
Рассмотрим треугольники ВМН и СМК.
Они прямоугольные по построению и имеют равные острые углы ( вертикальные при М- точке пересечения высот).
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Следовательно, вписанные ∠ С1СА=∠В1ВА и дуги, на которые они опираются, также равны.
⇒ дуга С1АВ1, равная 180°, делится точкой А на две равные дуги по 90°.
Вписанный угол АСС1 опирается на дугу 90°и равен половине ее градусной меры.
∠АСС1=45°
Треугольник СНА - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
Угол НАС=90°- 45°=45°
ответ: угол ВАС=45°
[email protected]