Объяснение:
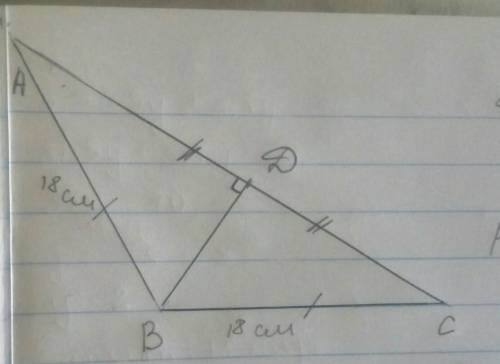
1) Т.к. АВ=ВС, то треугольник АВС-р/б, следовательно, ВD - медиана, биссектриса, высота.
Т.к. ВD - биссектриса, то в треугольнике АВD угол АВD= 120°:2=60°
Т.к. ВD - высота, то в треугольнике АВD угол АDВ = 90°
Сумма углов треугольника равна 180°, следовательно, угол ВАD = 180°-(60°+90°)=180°-150°=30°.
2) Мы узнали, что угол ВАD=30°, найдём длину ВD.
Треугольник АВD - прямоугольный.
В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы.
Угол ВАD = 30°, угол ВАD лежит напротив ВD, следовательно ВD = 0,5АВ=0,5×18=9 (см).
ответ: 1) 60°, 90°, 30°.
2) 9 см.
Вот чертёж, дано, надеюсь, напишешь.
Когда мы складываем вектора, мы образуем треугольник. (но вектора можно наложить друг на друга, а стороны треугольника - нет)
Значит, чтобы сумма векторов была наибольшей нужно, чтобы угол лежащий напротив него был наибольшим, То есть чтобы вектора были сонаправлены. (Наибольшая возможная угловая сумма треугольника 180°)
⇒ Мы просто из конца вектора A берём начало для вектора B и чертим два вектора (A и B) под углом 180°. (Допустим это вектор С)
С = А + В |A+B| = |C| |C| = | 29+18 | = 47
* Теперь просто из конца вектора A берем начало вектора В. Только теперь вектора противоположно направлены. И угол между ними 0°
С = А + В |A+(-B)| = |C| |C| = | 29+ (-18) | = | 29-18 | = 11
ответ: 11≤ |A+B| ≤47
Цилиндр, AK = KD = 3 (дм), S(ос.сеч.) = 72 (дм²).
Найти: S(пол), V, S(бок).
Решение:
Так как осевое сечение квадрат ABCD, то можно определить высоту
Диаметр основания в 2раза больше радиуса
AD = 2AK = 2*3 = 6 (дм)
Тогда S(ос.сеч.) = h*d, отсюда h
LK=S(ос.сеч)/AK = 72/6 = 12 (см).
Определяем площадь полной поверхности
S(пол) = 2π*AK*(AK+LK) = 2π*3*(3+12)=90π (см²).
Определяем площадь боковой поверхности
S(бок) = 2π*AK*LK = 2π*3*12 = 72π(см²).
Определяем объём
V = S(осн)*LK
S(осн) = π*AK² = 3²π=9π (см²)
V = S(осн)*LK = 9π*12=108π (см³).
ответ: S(пол) = 90π (см²), V=108π (см³), S(бок) = 72π (см²).