Рассмотрим диагональ трапеции МК и медиану треугольника РАК - КН . Диагональ проходит точку К и точку пересечения медиан, медиана также проходит точку К и точку пересечения медиан, значит медиана КС честь диагонали МК. Аналогично доказывается, что медиана РН - чеасть диагонали РЕ.
Точка Н делит РА попалам => МН - медиана в равнобедренном РАМ (РА=МА по условию) является и высотой и биссектрисой => МК перпендикулярна РА => КН медиана я вляющаяся и высотой в РКА => РК=КА
Аналогично доказывается с диагонолью РЕ:
РЕ перпендикулярно КА, РК=РА
Имеем Равносторонний РКА (РА=РК=КА) => РН=НА=АС=КС=РВ=КВ
Пусть РМН=АМН=х(т к МН - биссектриса)
По свойствам трапеции:
180=Р+М=2х+60+МРА (АРК=60 т к РКА - равносторонний)
МРА=90-х(по теореме об острых углах прямоуг. треугольника)
2х+90-х+60=180
х=30
(Аналогично с углами К и Е: СЕК=СЕА=30)
РМН=30
РН=sin30*РМ=sin30*a=a/2 Тогда
РН=НА=АС=КС=РВ=КВ=а/2
Тогда основание меньшее РК=РВ+КВ=а
Рассмотрим треугольники
СЕА и МНА
НА=АС
СЕА=30=АМН
То есть СЕА=МНА => АЕ=МА=а
КЕ=АЕ=а
ТОгда большее основание
МЕ=МА+АЕ=2а
Теперь осталось найти высоту трапеции
Приведем ее РН1
В треугольнике РМН1
РН1=РМ=РМ*sin60= 0.866а
И наконец
S=((A+B)/2)*h=(a+2a)/2 * 0.866а=0.14433а
ответ 0.14433а
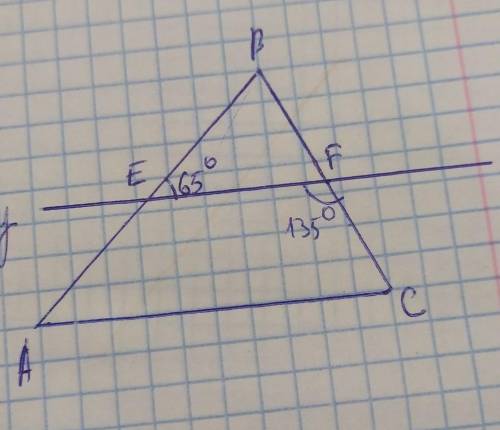
Угол A равен 65 градусов, угол B равен 70 градусов, угол C равен 45 градусов.
Объяснение:
Т. К. Углы BFE и EFC смежные, то угол бфе равен 180-135=45 градусов. Углы BEF и FEA смежные, значит угол феа равен 180-65=115 градусов. Рассмотрим треугольник EBF, т. К. Сумма всех углов равна 180 градусов. Тогда угол EBF равен 180-65-45=70 градусов. Рассмотрим две параллельные прямые EF и AC, секущая AB, тогда в углы EAC и BEF равны как соответственные, тоже самое и с другой стороны, только секущая BC. Тогда выясним, что угол EAC равен 65 градусов, а угол FCA 45 градусов.
Виды призм:прямая призма-призма, у которой все боковые рёбра перпендикулярны основанию.Правильная призма-призма в основании которой лежит правильный многоугольниу ,а боковые рёбра перпендекулярны плоскостям основания.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или высоту).
В прямой призме боковые ребра являются высотами.
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.