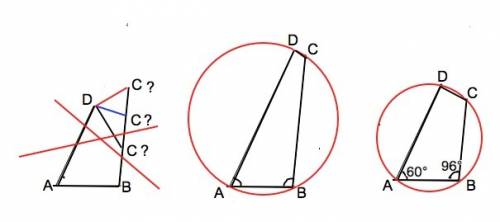
Задача имеет решение только если АВСD – четырехугольник, вписанный в окружность. (см. рисунки вложения)
В противном случае величину углов АDC и DCB вычислить невозможно, они могут принимать различное значения, лишь бы их сумма была равна разности между суммой углов четырехугольника и суммой углов АВС и BAD, т.е. 204°
-----------
Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º.
Тогда ∠ADC=180°-∠ABC=180°-96=84°
∠BCD=180°-∠BAD=180°-60°=120°⇒
∠BCD-∠ADC=120°-84°=36°.
2) Если не принимать во внимание слово "прямоугольный":
угол при основании равен 90 - (120/2) = 90 - 60 = 30 градусов.
Отсюда радиус основания как проекция образующей на основание равен r = 16*cos 30° = 16*√3/2 = 8√3 см.
Площадь основания So = π*64*3 = 192π см².
Площадь боковой поверхности Sбок = πrl = π*8√3*16 = π*128√3 см².
Полная поверхность равна:
S = Sо + Sбок = 192π + π*128√3 = 64π(3+2√3) см².
3) Из площади основания находим радиус:
64 = πr²,
r = √(64/π) = 8/√π дм.
А так как осевое сечение - прямоугольник, то его высота (это высота цилиндра) равна Н = 12√π / (2r) = 12√π/(16/√π) = 3π/4 дм.
4) Разность радиусов оснований равна проекции образующей на основание.
r2 - r1 = √(10² - 8²) = √(100 - 64) = √36 = 6 см.
Площадь боковой поверхности Sбок = π(r1+r2)l.
Отсюда r1+r2 = Sбок/(πl) = 120π/(π*10) = 12 см.
Радиус большего основания r2 = r1+ 6,
тогда r1 + (r1 + 6) = 12, то есть 2r1 = 6, отсюда r1 = 6/2 = 3 см.
Второй радиус r2 = 12 - 3 = 9 см.
Радиусы перпендикулярны общей касательной.
Если от большого радиуса отнять малый, то получим прямоугольный треугольник с катетом 8-2=6 и вторым, равным АВ.
Расстояние АВ = √(10²-6²) = √(100-36) = √64 = 8.