Вписанные углы РMN и KNM опираются на равные хорды. Следовательно, дуги, стягиваемые этим хордами, равны. Вписанные углы, опирающиеся на равные дуги (или на равные хорды), равны.
∠РMN=∠KNM
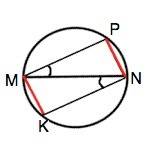
Проведем хорды МР и КN.
В треугольниках MPN и MKN вписанные ∠Р = ∠К (опираются на диаметр).⇒
Прямоугольные ∆ МРN=∆ MKN по острому углу и общей гипотенузе.
Отсюда следует равенство PNM=KMN
Эти углы - накрестлежащие при пересечении РN и MK секущей MN.
Если при пересечении двух прямых секущей накрестлежащие углы равны. эти прямые - параллельны. Доказано.
Для ответа на вопрос, поставленный задачей, достаточно рассмотреть данный во вложении рисунок.
К стороне СD пристроен равносторонний треугольник CDE, все углы которого равны 60°, а стороны СЕ=DE=CD.
Точка Е не может находиться на стороне квадрата АВ, так как в таком случае получившийся треугольник равносторонним не будет.
∠АDE= ∠ADC+∠CDE=90°+60°=150°
Так как СD- сторона данного в условии квадрата, то
АD=DE,
и треугольник ADE- равнобедренный с углами при основании АЕ=15 градусов.
Так как ∠ СЕD=60°,
∠ АЕС=60°-15°=45°
а = 18х + 7х = 25х
высота образует два прямоугольных треугольника
и по т.Пифагора можно записать:
с² = 48² + (18х)²
а² = (25х)² = 48² + (7х)²
(25х)² - (7х)² = 48²
(25х-7х)(25х+7х) = 48²
18х*32х = 48²
х² = 48*48/(18*32) = 6*8*6*8/(6*3*8*4) = 4
х = 2
тогда а = 25*х = 50
с² = 48*48 + 18*2*18*2 = 6*8*6*8 + 6*3*4*6*3 = 6*6*4*(16+9) = (6*2*5)²
с = 60