АС=ВД=5,4см
Объяснение:
обозначим вершины прямоугольника ABCD с диагоналями АС и ВД а точку их пересечения О. Каждая диагональ делит прямоугольник на 2 равных прямоугольных треугольника АВС и АСД, в которых стороны прямоугольника являются катетами а диагонали гипотенузами. Обозначим пропорции 1:2 как х и 2х. Пусть <САД=х, а <ВАС=2х и зная, что диагональ делит прямой угол равный 90°, составим уравнение:
х+2х=90
3х=90
х=90÷3=30°.
Итак: <САД=30°, тогда катет СД, лежащий напротив него равен половине гипотенузы поэтому АС=2×2,7=5,4см
Так как диагонали прямоугольника равны, то АС=ВД=5,4см
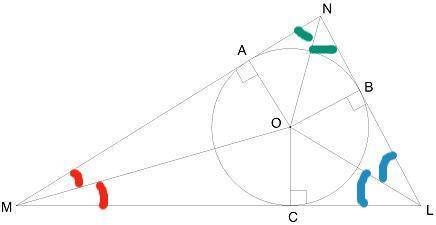
< COA = 128°, < BOA = 124°, < COB = 108°
Объяснение:
Центр окружности, вписанной в треугольник, находится на пересечении биссектрис углов треугольника. Поэтому OM, ON и OL - биссектрисы.
Биссектриса делит угол пополам - значит, < OML = < OMN = 26°,
< ONM = < ONL = 28°.
Сумма углов треугольника 180°.
В треугольниках ΔCOM, ΔMOA углы < OCM = 90°, < OAM = 90°.
Тогда < COM = 180° - < OML - < OCM = 180° - 26° - 90° = 64°
< AOM = 180° - < OMN - < OAM = 180° - 26° - 90° = 64°
( * ) < COA = < COM + < AOM = 64° + 64° = 128°
В треугольниках ΔAOM, ΔMOB углы < OBN = 90°, < OAN = 90°.
Тогда < AON = 180° - < ONM - < OAN = 180° - 28° - 90° = 62°
< AOM = 180° - < OMN - < OAM = 180° - 28° - 90° = 62°
( * ) < BOA = < BON + < AON = 62° + 62° = 124°
< COA + < BOA + < СOB = 360° (эти углы составляют полный угол)
< COB = 360° - < COA - < BOA = 360° - 128° - 124° = 108°
Найти периметр треугольника.
Решение. Пусть АВ=ВС=х, тогда по теореме Пифагора из треугольника АВК: АК=√(х²-400)
АС=2АК=2√(х²-400).
Площадь треугольника S=(АС·ВК)/2 и S=(BC·AM)/2.
Значит
АС·ВК=ВС·АМ,
2·√(х²-400)·20=24·х,
100(х²-400)=36х²,
х²=625.
х=25
АВ=ВС=25
АС=2√625-400=2·15=30
Периметр Р= АВ+ВС+АС=25+25+30=80
2)была решена ранее