Расстояние равно √433,0625 ≈ 20,8 см.
Объяснение:
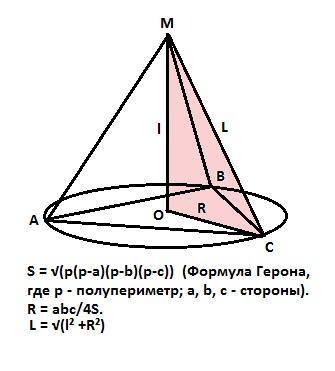
Соединим точку М с вершинами данного треугольника. Получится пирамида, вершина которой проецируется в центр описанной вокруг треугольника окружности, так как если наклонные (расстояния от М до вершин) равны, то равны и их проекции (радиус описанной окружности).
Найдем площадь данного нам треугольника по формуле Герона, где р - полупериметр треугольника, a,b,c - его стороны:
S = √(p(p-a)(p-b)(p-c)) = √(42·16·14·12) = 336cм².
Формула радиуса описанной окружности:
R = a·b·c/4·S = 26·28·30/(4·336) = 16,25см.
Искомое расстояние находим по Пифагору:
L= √(МО²+R²) =√(13²+16,25²) = √433,0625 ≈ 20,8 cм.
CK = HK/cos30 = 5/v3/2 = 10v3/3
CK = cos30*DK
DK = CK/cos30 = 10v3/3/v3/2 = 10*2/3 = 20/3 = 6 2/3