Якщо ще актуально)
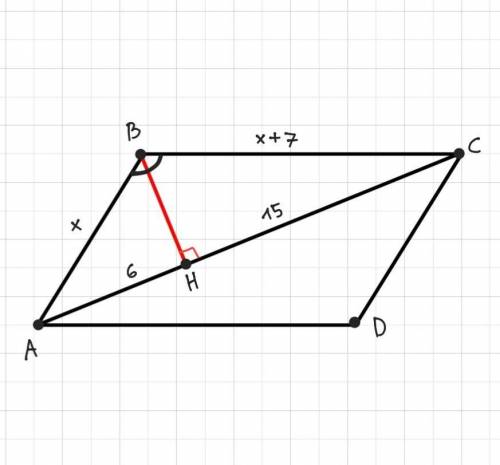
Дано: ABCD - паралелограм, АС - діагональ, ВН⟂АС, АН= 6 см, СН= 15 см, ВС–АВ= 7 см.
Знайти: S abcd.
Розв'язання.
Розглянемо трикутники АНВ і СНВ.
Вони прямокутні, а сторона ВН для них є спільним катетом. АН= 6 см, СН= 15 см, тому очевидно, що ВС>АВ.
Нехай АВ= х см, тоді ВС= (х+7) см.
Оскільки ВН - спільна сторона, тоді справедлива така рівність (через т.Піфагора у ΔAHB і ΔCHB):
АВ²–АН²= ВС²–НС²;
х²–6²= (х+7)²–15²;
х²–6²= х²+14х+49–225;
х²–х²–14х= 36+49–225;
–14х= –140;
14х= 140;
х= 10 (см)
Отже, АВ= 10 см, тоді:
ВН²= х²–6²= 10²–6²= 100–36= 64;
ВН= 8 см (–8 не може бути)
Розглянемо ΔABC:
AC= AH+HC= 6+15= 21 см
ВН= 8 см, ВН - висота ΔABC, оскільки ВН⟂АС.
Знайдемо площу ΔАВС:
S= ½•AC•BH;
S= ½•21•8= 84 (см²).
Діагоналі паралелограма ділять його на два рівних трикутники, тобто їх площі рівні.
SΔABC= SΔCDA= 84 см²
Звідси площа паралелограма ABCD дорівнює
S abcd= 2•SΔABC= 2•84= 168 (см²).
Відповідь: 168 см².
Якщо ще актуально)
Дано: ABCD - паралелограм, АС - діагональ, ВН⟂АС, АН= 6 см, СН= 15 см, ВС–АВ= 7 см.
Знайти: S abcd.
Розв'язання.
Розглянемо трикутники АНВ і СНВ.
Вони прямокутні, а сторона ВН для них є спільним катетом. АН= 6 см, СН= 15 см, тому очевидно, що ВС>АВ.
Нехай АВ= х см, тоді ВС= (х+7) см.
Оскільки ВН - спільна сторона, тоді справедлива така рівність (через т.Піфагора у ΔAHB і ΔCHB):
АВ²–АН²= ВС²–НС²;
х²–6²= (х+7)²–15²;
х²–6²= х²+14х+49–225;
х²–х²–14х= 36+49–225;
–14х= –140;
14х= 140;
х= 10 (см)
Отже, АВ= 10 см, тоді:
ВН²= х²–6²= 10²–6²= 100–36= 64;
ВН= 8 см (–8 не може бути)
Розглянемо ΔABC:
AC= AH+HC= 6+15= 21 см
ВН= 8 см, ВН - висота ΔABC, оскільки ВН⟂АС.
Знайдемо площу ΔАВС:
S= ½•AC•BH;
S= ½•21•8= 84 (см²).
Діагоналі паралелограма ділять його на два рівних трикутники, тобто їх площі рівні.
SΔABC= SΔCDA= 84 см²
Звідси площа паралелограма ABCD дорівнює
S abcd= 2•SΔABC= 2•84= 168 (см²).
Відповідь: 168 см².

На продолжении медианы АМ за точку М отложим отрезок МК, равный АМ. АМ=МК=15, РК=РМ+МК=10+15=25
Полученный четырехугольник АСКВ-параллелограмм, т.к. его диагонали АК иВС точкой пересечения М делятся пополам (ВМ=МС и АМ=МК).
Пусть АС=СВ=ВК=х, тогда
ΔАРН подобен ΔВРК по двум углам (угол АРН=углу ВРК, угол АНР=ВРК=90), тогда АР/РК=5/25=1/5 и АН/ВК=НР/РВ=1/5
Отсюда АН=ВК/5=х/5
Из прямоугольного ΔВРК РВ²=РК²-ВК²=25²-х²=625-х²
РВ=√(625-х²)
Т.к. НР/РВ=1/5, НР=РВ/5=1/5√(625-х²)
НВ=РВ+НР=√(625-х²)+1/5√(625-х²)=6/5√(625-х²)
Из прямоугольного ΔАВН
АВ²=НВ²+АН²=(6/5√(625-х²))²+х²/25=(36(625-х²)+х²)/25
В параллелограмме D²+d²=2(a²+b²), значит
АК²+СВ²=2(АС²+АВ²) или АК²+АС²=2АС²+2АВ²
30²=АС²+2АВ²,
АВ²=(30²-х²)/2=(900-х²)/2
Приравниваем АВ²:
(36(625-х²)+х²)/25=(900-х²)/2
2(36(625-х²)+х²)=25(900-х²)
45000-72х²+2х²=22500-25х²
22500=45х²
х²=500
тогда АВ²=(900-х²)/2=(900-500)/2=200
АВ=√200=10√2