Прямой параллелепипед
Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота параллелепипеда
Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания
Объём V=Sо*h
1.
D^2=Dосн^2 +h^2
Половина основания -это треугольник.
Площадь треуг. по формуле Герона
где р- полупериметр, a b c -стороны= 10 17 21р=(10+17+21) /2Sосн=2S=h= V (D^2-Dосн^2)= V (29^2-21^2)=
Sполн= 2*Sосн+Sб=2*()+2*(10+17)*h=...
2.Найдем длину диагонали по теореме косинусов
Dосн =V 3^2+8^2 -2*3*8 *cos60 =
потом площадь основания аналогично 1.
потом полную поверхность аналогично 1.
площадь S меньшего диагонального сечения= Dосн*h
где h=Sб /Росн
3.Sосн=1/2*d1*d2=1/2*6*8=24
сторона ромба b = V (6/2)^2 +(8/2)^2= 5
высота паралл h= V D^2 - b ^2 = V 13^2 -5^2 = 12
все данные есть
потом полную поверхность аналогично 1.
Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
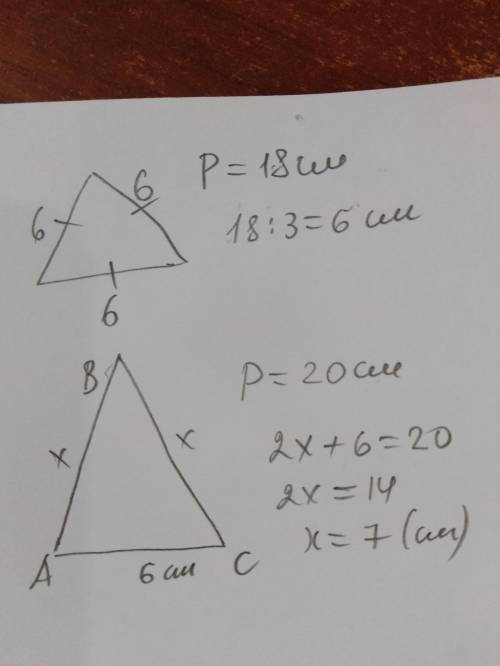
если в трапеции провести высоту, то получим прямоугольный треугольник и по т.Пифагора можно записать:
(25+х)² = 40² + (25-х)²
(25+х)² - (25-х)² = 40²
(25+х - 25+х)(25+х + 25-х) = 40²
2х*50 = 40²
х = 16
Периметр трапеции = (20+25) + (20+20) + (20+16) + (16+25) = 162