∠B = 30°
Пояснение:
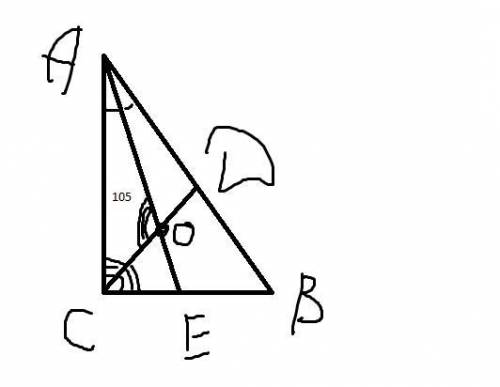
Дано: Δ АВС, ∠С = 90°, ∠АОС = 105°, биссектрисы CD и АЕ, что пересекаются в точке О
Найти: меньший острый угол Δ АВС
Решение
∠CAO = ∠OAD (так как биссетриса AE делит угол ∠А пополам)
∠ACD = ∠OCB= ∠C/2 = 90°/2 = 45° (так как биссетриса CD делит угол ∠C пополам)
Рассмотрим Δ CAO, в котором ∠CAO = 45°, ∠АОС = 105°, ∠CAO - ?
Так как сумма всех углов в треугольнике равна 180°, то
∠CAO = 180° - (105° + 45°) = 180° - 150° = 30°
∠CAO = ∠OAD = 30°, следовательно ∠А = ∠CAO + ∠OAD = 60°
Рассмотрим Δ АВС, в котором ∠С = 90°, ∠А= 60, ∠B - ?
Так как сумма углов при катетах в прямоугольном треугольнике равна 90°, то
∠B = 90° - ∠А = 90° - 60° = 30°
ответ: ∠B = 30°
Сторони паралелограма будуть 10см; 10см; 12см; 12см;
Объяснение:
Щоб найти площу паралелограма потрібно сторону помножити на висоту, тобто S=ah, а нам відомо, що висота у 4 рази менша, значить сторона на яку вона спираєть буде у 4 рази більша і в нас є площа і можна найти висоту і тут буде рівняння ( відчуваю себе розумною). 36=4х * х; 36=4х2; 9=х2; 3=х - ми найшли висоту.
Тоді сторона буде 3*4=12 а протилежні сторони рівні
тоді від периметра віднімаємо дві сторони 44-12-12=20 знайшли дві ще сторони і ділемо на два
20:2=10
Все
Док-во: продолжим прямую АС и отметим на ней точку К, АС=СК. Треугольники АВС и ВСК равны (по двум катетам - признак равенства прямоугольных треугольников). Тогда равны и стороны АВ и ВК. То есть треугольник АВК - равносторонний ( все углы по 60 град) и ВС является одновременно высотой, медианой и биссектрисой. То есть угол АВС=половине угла АВК = 60:2=30 град. ч.т.д.
2) Дано: АВС, СК - медиана к стороне АВ, т.е.АК=КВ. По условию СК=1/2*АВ=АК. Имеем два равнобедренных треугольника АКС и КСВ. Углы при основании равнобедренных треугольников равны(уг.САК=уг.АСК=α уг.КСВ=уг.СВК=β), Сумма углов треугольника =180 град 2α+2β=180
2(α+β)=180 α+β=90. То есть угол С=α+β=90 град.