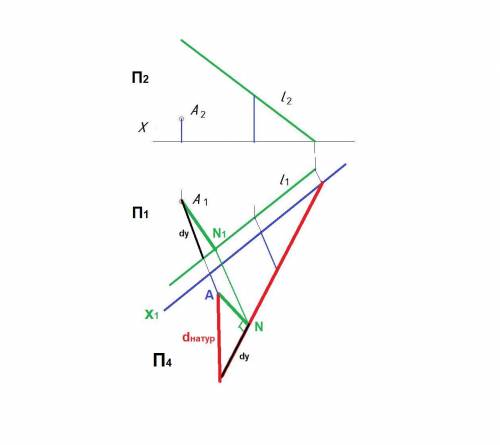
Надо перевести прямую в положение, параллельное плоскости проекции. Для этого используется метод замены плоскостей, который не предполагает перемещение фигур в пространстве.
Параллельно проекции l введена дополнительная фронтальная плоскость П4. В новой системе (П1, П4) точки находятся на том же удалении от оси X1, что и на фронтальной проекции.
Далее опускаем перпендикуляр из А1 на прямую l1, поскольку прямой угол проецируется на плоскость П4 в натуральную величину. По линии связи определяем положение точки N' и проводим проекцию A'N' отрезка AN.
На заключительном этапе определяем величину отрезка AN по его проекции на плоскости П4 и dy. Для этого строим прямоугольный треугольник, у которого катет равен разности dy удаления точек A и N от оси X1. Длина гипотенузы треугольника соответствует искомому расстоянию от A до l.
1.
По теореме косинусов найдём угол MON
MN² = OM² + ON² - 2*OM*ON*cos(∠MON)
12² = 20² + 20² - 2*20*20*cos(∠MON)
144 = 400 + 400 - 800*cos(∠MON)
656 = 800*cos(∠MON)
cos(∠MON) = 41/50
∠MON = arccos(41/50)
2.
Площaдь треугольника MON
S(ΔMON) = 1/2*OM*ON*sin(∠MON)
sin(∠MON) = √(1-cos²(∠MON)) = √(1 - 41²/50²) = √(2500 - 1681)/50 = √819 / 50 = 3√91/50
S(ΔMON) = 1/2*20*20*3√91/50 = 12√91
3.
Площадь кругового сектора MON
S(∪MON) = ON²*∠MON/2 = 20²/2*arccos(41/50) = 200*arccos(41/50)
4.
Площадь заштрихованной фигуры
S = S(∪MON) - S(ΔMON) = 200*arccos(41/50) - 12√91 ≈ 7.404
С отношении косинусов определим катет
Cos угла - это отношение прилежащещего катета к гипотенузе., тоесть
Значит катеты будут
Определим площадь