Дано:
ABCDA₁B₁C₁D₁ - куб
AB = 2
--------------------------------
Найти:
а) р(B, A₁C₁) - ?
б) р(A, BD₁) - ?
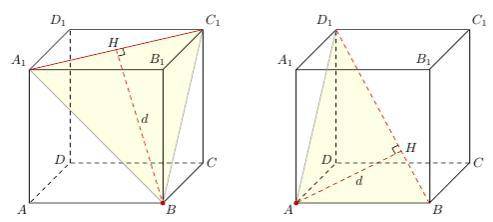
а) Проведем BH⊥A₁C₁. Искомое расстояние BH = d есть высота BH - ΔBA₁C₁. ΔA₁BC₁ равносторонний — все его стороны, будучи диагоналями граней, равны ⇒ A₁B = BC₁ = √2, cледовательно:
sin∠BA₁H → BH/BA₁ → BH = BA₁ × sin60° = √2 × √3/2 = √6/2 ⇒ BH = р(B, A₁C₁) = √6/2
(Рисунок показан внизу где влево).
б) Проведем BH⊥BD₁ Искомое расстояние AH = d есть высота AH - ΔABD₁. ΔABD₁ - прямоугольный. Действительно, прямая AB⊥(ADD₁) и поэтому перпендикулярна любой прямой, лежащей в этой плоскости — в частности, прямой AD₁.
Имеем: AB = 2, AD₁ = √2, BD₁ = √3
Если S — площадь треугольника ABD₁, то получаем:
2S = AB×AD₁ = BD₁×AH ⇒ AH = AB×AD₁/BD₁ = 2×√2/√3 = 2√2/√3 × √3/√3 = 2√2×3/(√3)² = 2√6/3 ⇒ р(A, BD₁) = AH = 2√6/3
(Рисунок показан внизу где вправо).
ответ: а) р(B, A₁C₁) = √6/2, б) р(A, BD₁) = 2√6/3
Дано:
ABCDA₁B₁C₁D₁ - Прямоугольный параллелепипед
∠ABD=60°
CC₁ = 8см
AB = 15см
----------------------------------------------------------------------------
Найти:
V(ABCDA₁B₁C₁D₁) - ?
Сначала мы находим сторону основания AD этого прямоугольника ABCD:
ΔABD - прямоугольный (∠BAD = 90°, и ∠ABD=60°) ⇒ tg∠ABD = AD/AB ⇒
AD = AB × tg∠ABD = 15 см × tg60° = 15 см × √3 = 15√3 см
И теперь мы находим объем прямоугольного параллелепипеда:
V(ABCDA₁B₁C₁D₁) = Sосн × h = S(ABCD) × СС₁ = AB×AD×CC₁ = 15 см × 15√3 см × 8 см = 225√3 см² × 8 см = 1800√3 см³
ответ: V(ABCDA₁B₁C₁D₁) = 1800√3 см³
P.S. Рисунок показан внизу↓

Нехай сторона основи буде х см, а бічна сторона - (х+1) см. Периметр трикутика дорівнює 20 см. Знаходимо сторону рывнобедреного трикутника
Тоді сторони рівнобедреного трикутника будуть
Відповідь: 6 см, 7см і 7см.