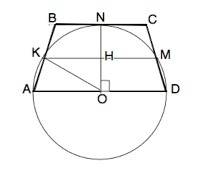
Проведем радиус ON в точку касания с ВС.
NO⊥ВС, ⇒ NO⊥AD,
КМ - средняя линия и делит пополам высоту трапеции – радиус NO.
NO=R=d:2=5
ОН= NO:2=2,5
NO перпендикулярна ВС и AD.⇒
NO⊥КМ, а КМ здесь - хорда.
Радиус, перпендикулярный хорде, делит ее пополам.
КН=МН.
Из ∆ КОН по т.Пифагора
КН=√(КО²-ОН²)=√(25-6,25)=2,5√3⇒
КМ=2•2,√5=5√3
Из ∆ КОН sinKOH=KH:KO=(2,5√3):5=√3/2 - это синус 60°
Тогда ∠КОА=90°-60°=30°
ОК=ОА ( радиусы) ∆ КОА- равнобедренный.⇒
Углы при основании равнобедренного треугольника равны.
∠КАО=∠АКО= (180°-30°):2=75°
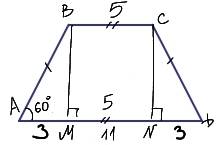
В треугольнике АВС <A=120*.
Обозначим <B=a, тогда <C=180*-120*-a=60*-a.
Внешний угол при вершине В равен 180*-а,
внешний угол при вершине С равен 180*-(60*-а)=120*+а.
В треугольнике ОВС <OBC=(180*-a):2=90*-a/2,
<OCB=(120*+a):2=60*+a/2.
<ВOС=180*-(90*-a/2)-(60*+a/2)=180*-90*+a/2-60*-a/2=30*
ответ: 30*