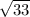Рассмотрим основание пирамиды - это квадрат, так как пирамида правильная. Диагональ квадрата делит его на два равносторонних прямоугольных треугольника с катетами по 8 см.
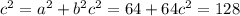
c=8 корней из 2 - это длина диагонали. Точка пересечения диагоналей делит их пополам и с/2=4 корня из 2.
Рассмотрим треугольник, сторонами которого являются половина диагонали, высота пирамиды и ее ребро. Этот треугольник прямоугольный, так как присутствует высота. Ищем гипотенузу - ребро пирамиды по теореме Пифагора
с в квадрате = 100 + (4 корня из 2) в квадрате
с в квадрате = 100+32=132
с=2 корня из 33 (см)
ответ: 2 корня из 33 см длина ребра
Т.К. АВ || CD И AF - СЕКУЩАЯ, ТО∠АFD = ∠BAF, ПОЛУЧИЛИ ЧТО В ТРЕУГОЛЬНИКАХ AGD И FGD ДВА УГЛА РАВНЫ МЕЖДУ СОБОЙ, ЗНАЧИТ И ТРЕТЬИ УГЛЫ ТОЖЕ РАВНЫ, Т.Е. ∠AGD =∠FGD. ∠AGE = ∠FGD Т.К. ОН ВЕРТИКАЛЬНЫЕ. ПОЛУЧИЛИ ∠AGD =∠FGD = ∠AGE. ЗНАЧИТ ∠EGF РАВЕН КАЖДОМУ ИЗ ТРЕХ. Т.О ВСЕ ЧЕТЫРЕ УГЛА РАВНЫ. ЗНАЧИТ 360° : 4 = 90°. СЛЕДОВАТЕЛЬНО AF ⊥ DE.
Δ AGD = Δ FGD ПО ОБЩЕЙ СТОРОНЕ GD И РАВНЫХ УГЛАХ ADG И GDF, AGD И FGD ПОЛУЧИМ, ЧТО AG = GF.
Пусть ABCD- квадрат в основании пирамиды, О- его центр, F -Вершина.
Высота пирамиды соответственно OF = 10, AB=BC=CD=AD=a=8
Рассмотрим прямоугольный треугольник AOF.
AO - половина диагонали основания.AO=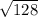 /2
/2
тогда AF=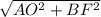 =
= 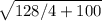 =
= 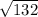 = 2
= 2