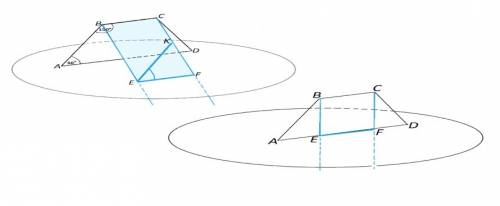
1) Каково взаимное расположение прямых EF и AB?
(Уточняем - в плоскости α лежит только АД, а ВС - не лежит).
ВС параллельна АD ⇒ параллельна плоскости α.
АD параллельна ВС, ЕF параллельна ВС. Две прямые , параллельные третьей прямой, параллельны. ⇒
ЕF ║ АD и параллельна плоскости АВСD, но не параллельна АВ, которая пересекается с АD. ⇒
Прямые EF и AB - скрещивающиеся.
2) Чему равен угол между прямыми EF и AB, если ABC = 150°?
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Сумма углов при боковой стороне трапеции 180°, следовательно, ∠ВАD=180°-150°=30°.
Проведем в плоскости ВЕF прямую ЕК║ АВ.
ЕК|║АВ; ЕF║АD Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.⇒
∠FЕК=∠ВАD=30°
-----------
ВЕ и СF могут быть проведены в плоскости АВСD.
Тогда ЕD будет лежать на АD и в этом случае непараллельные прямые EF и АВ лежат в одной плоскости. Тогда АВ и EF пересекyтся.
Дан параллелограмм ABCD
BE - высота к AD = 4 см
BF - высота к CD = 3 см
угол BAE = 30 ⁰
Найти
S (abcd) - ?
Решение.
1) рассмотрим ΔABE - прямоугольный, т.к. BE высота.
угол BEA - 90⁰, BAE - 30⁰ ⇒ ABE - 60⁰
В тр. с углами 30, 60, 90 - катет лежащий против угла в 30 равен половине гипотенузы ⇒ AB=2BE=2*4=8 см
2) рассмотрим ΔBFC - прямоугольный, т.к. BF высота.
угол BFC - 90⁰, BCF - 30⁰ (свойство углов параллелограмма) ⇒ FBC - 60⁰
В тр. с углами 30, 60, 90 - катет лежащий против угла в 30 равен половине гипотенузы ⇒ BC=2BF=2*4=8 см
3) S=a*b*Sinα
S=6*8*Sin30=48*(1/2)=24 см²
или
S=b*h (BC*BE)
S=6*4= 24 см²
или
S=a*h (AB*BF)
S=8*3=24 см²
ответ. площадь параллелограмма 24 см²
bc=180°-ab=180°-40°=140°