Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.
Свойства
1Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
2Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
3Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с радиусом, является тангенсом угла между этим радиусом и направлением от центра окружности на точку касания. «Тангенс» от лат. tangens — «касательная».
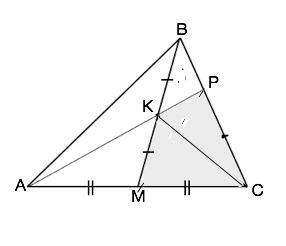
Медиана треугольника делит его на два равновеликих.
ВМ- медиана ∆ АВС.
Ѕ(АВМ)=Ѕ(СВМ)
АК- медиана ∆ АВМ.
Ѕ(АВК)=Ѕ(АМК)=Ѕ(АВК):2
Рассмотрим ∆ МВС с пересекающей его АР.
По т.Менелая 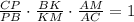
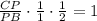 ⇒
⇒
СР:РВ=2:1
В ∆ МВС и ∆ ВКР угол В - общий.
Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.
Пусть ВР=х, ВК=у, тогда ВС=3х, ВМ=2у
Ѕ(МСВ):Ѕ(ВКР)=(2у•3х):ух=6:1
Примем Ѕ(ВКР)=а
Тогда Ѕ(ВМС)=6а, а Ѕ(КРСМ)=6а-а=5а
Т.к. Ѕ(АВМ)=Ѕ(ВСМ), то Ѕ(АВС)=2Ѕ(ВСМ=12а ⇒
Ѕ(АВС):Ѕ(КРСМ)=12а:5а=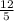
———————
Из найденного можно найти отношение площадей любых частей ∆ АВС. Например, отношение S(ABK) ( или равновеликого ему ∆ АКМ) к площади четырехугольника KPCM равно 3а:5а=0,6
или
Ѕ(КРСМ):Ѕ(АВК)=5:3
Пусть дана трапеция ABCD, AD=28, BC=21
В трапецию можно вписать окружность, если сумма противоположных сторон равна. то есть AD+BC=AB+CD
Опустим с вершины B трапеции на основание BK высоту BK, тогда
AK=AD-KD=28-21=7
Пусть высота трапеции BK=x, тогда
(AB)^2=(BK)^2+(AK)^2=x^2+7^2
AB=sqrt(x^2+7^2)
Так как
AD+BC=AB+CD, то
21+28=x+sqrt(x^2+7^2)
sqrt(x^2+7^2)=49-x
x^2+7^2=(49-x)^2
x^2+49=2401-98x+x^2
98x=2352
x=24, то есть высота трапеции равна 24
R=H/2
R=24/2=12 - радиус вписанной окружности