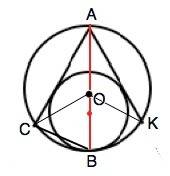
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. ⇒
∠САВ=∠КАВ=60°:2=30°
∠АСВ=∠АКВ=90°- опираются на диаметр АВ.
Прямоугольные ∆ АСВ=∆ АКВ по острому углу при А и общей гипотенузе АВ. ⇒
АС=AK=АВ•cos30°=2R*√3:2=R√3
* * *
Как вариант - СВ противолежит углу 30° и равен R, можно применить т.Пифагора,
или провести радиус ОС и находить АС из равнобедренного ∆ АОС по т.косинусов.
В равнобедренном треугольнике биссектрисы, проведённые к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его биссектрисы. Треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, углы LAB и KBA равны как углы при основании равнобедренного треугольника, а углы LBA и KAB равны как половины углов при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB - биссектрисы треугольника ABC - равны. Теорема доказана.
Теорема d3. В равнобедренном треугольнике высоты, опущенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его высоты. Тогда углы ABL и KAB равны, так как углы ALB и AKB прямые, а углы LAB и ABK равны как углы при основании равнобедренного треугольника. Следовательно, треугольники ALB и AKB равны по второму признаку равенства треугольников: у них общая сторона AB, углы KAB и LBA равны по вышесказанному, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Если треугольники равны, их стороны AK и BL тоже равны. Что и требовалось доказать.
12.4-0.8=11.6 ( дм) другая сторона параллелограмма.
Р= 2×(12.4+11.6)= 2×24=48 см²
___
2)
12.4+1.6=14 ( дм ) другая сторона параллелограмма.
Р= 2× (12.4+14)=2×26.4=52.8 см²
___
3)
12.4÷4=3.1( дм ) другая сторона параллелограмма.
Р= 2×(12.4+3.1)= 2× 15.5 =31 см²