т.к. площадь всей поверхности равна 108,а площадь боковой поверности 60,то площадь основания равна 48,а так же равна a^2/4,тогда а-длина ребра основания равна 8
т.к. площадь боковой поверхности равна 60,а так же ранвна Pосн*h/2,где h-апофема,,а Pосн=3a,то h=5,т.к пирамида правильноя,то боковые грани равны,и являются равнобедренными треугольниками,тогда h-медиана,тогда
Хорошо, для начала давайте разберемся, что такое боковая поверхность и полная поверхность правильной треугольной пирамиды.
Боковая поверхность - это общая площадь боковых граней пирамиды. В нашем случае, боковая поверхность равна 60√3 см^2.
Полная поверхность - это площадь всех граней пирамиды, включая основание. В нашем случае, полная поверхность равна 108√3 см^2.
Теперь давайте решим задачу. Пусть a - длина стороны основания пирамиды, h - высота боковой грани пирамиды, и l - длина бокового ребра.
У правильной треугольной пирамиды у нас есть 4 боковые грани, каждая из которых является равнобедренным треугольником, у которого две стороны длиной a и третья сторона длиной l.
Теперь мы можем использовать формулы для нахождения площади поверхности пирамиды:
Площадь боковой поверхности боковой грани = (1/2) * a * h
Площадь основания пирамиды = (a^2 * √3) / 4
Теперь мы можем записать уравнения для нахождения a и h, и затем использовать эти значения для нахождения l.
1) Площадь боковой поверхности = (1/2) * a * h
Из условия задачи мы знаем, что площадь боковой поверхности равна 60√3 см^2, поэтому 60√3 = (1/2) * a * h
2) Площадь основания = (a^2 * √3) / 4
Из условия задачи мы знаем, что полная поверхность равна 108√3 см^2, поэтому 108√3 = (a^2 * √3) / 4
Теперь давайте решим эти уравнения.
1) 60√3 = (1/2) * a * h
У нас нет информации о значении h, поэтому нам не удастся найти точные значения для a или h без дополнительной информации.
2) 108√3 = (a^2 * √3) / 4
Если мы домножим обе части уравнения на 4, мы получим:
432√3 = a^2 * √3
Делая квадратный корень от обеих частей уравнения, мы получим:
a = √432
a = 12√3
Теперь давайте найдем длину бокового ребра пирамиды, l, используя теорему Пифагора:
l^2 = a^2 + h^2
Мы уже знаем значение a = 12√3, и нам необходимо найти значение h. У нас нет непосредственной информации о h, однако мы можем использовать площадь основания пирамиды, чтобы решить это.
Площадь основания пирамиды = (a^2 * √3) / 4
108√3 = (12√3)^2 * √3 / 4
108√3 = (144 * 3) * √3 / 4
108√3 = 432√3 / 4
Перемножим обе части уравнения на 4:
432√3 = 432√3
Итак, мы получили равенство, которое означает, что мы ошиблись в предположении о значении a = 12√3. Это значит, что мы не можем найти точное значение длины бокового ребра пирамиды без дополнительной информации.
В заключении, мне жаль, но без дополнительных данных мы не можем ответить на вопрос о длине бокового ребра правильной треугольной пирамиды.
т.к. площадь всей поверхности равна 108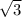 ,а площадь боковой поверности 60
,а площадь боковой поверности 60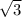 ,то площадь основания равна 48
,то площадь основания равна 48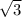 ,а так же равна a^2
,а так же равна a^2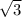 /4,тогда а-длина ребра основания равна 8
/4,тогда а-длина ребра основания равна 8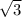
т.к. площадь боковой поверхности равна 60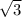 ,а так же ранвна Pосн*h/2,где h-апофема,,а Pосн=3a,то h=5,т.к пирамида правильноя,то боковые грани равны,и являются равнобедренными треугольниками,тогда h-медиана,тогда
,а так же ранвна Pосн*h/2,где h-апофема,,а Pосн=3a,то h=5,т.к пирамида правильноя,то боковые грани равны,и являются равнобедренными треугольниками,тогда h-медиана,тогда
b-бокове ребро найдем по теореме Пифагора b=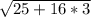 =
=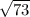 см
см