При симметрии относительно плоскости ОХУ координаты х и у точки не изменятся, а координата z поменяет знак на противоположный, так как симметричная точка будет находиться на таком же расстоянии от плоскости ОХУ, но с другой стороны.
Тогда центр сферы, точка с координатами (4; –2; 1) перейдёт в точку с координатами (4; –2; –1).
Уравнение сферы: (х – а)² + (у – b)² + (z – c)² = R²
(a; b; c) – координаты центра сферы, R – радиус сферы.
Тогда уравнение сферы с центром в точке с координатами (4; –2; –1) и радиусом 3 см примет вид:
(х – 4)² + (у + 2)² + (z + 1)² = 3²
(х – 4)² + (у + 2)² + (z + 1)² = 9
Найдём объём шара:
V = 4/3∙πR³
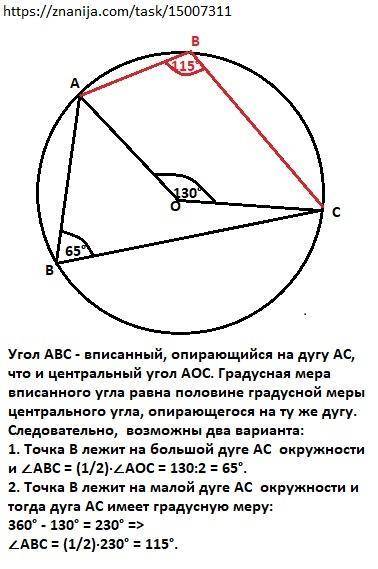
V = 4/3∙π·3³ = 4∙π·9 = 36π1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
ответ: 55, 55, 125, 125 градусов.