sinA = -0,8 => имеем прямоугольный треугольник со сторонами 6, 8, 10, откуда следует,что cosA = 0,6. Можно рассматривать два случая: 270>A>90 либо 360>A>270. В первом случае cosA= -0,6, во втором cosA = 0,6
Из прямоугольных ∆ СВВ1 и ∆САА1 с общим острым углом С
cos C=В1С:ВС=А1С:АС
По первой лемме о высотах –
(Если в треугольнике ABC нет прямого угла, AA1 и BB1 – его высоты, то ∆ А1В1С подобен ∆ ABC., т.е. если соединить основания двух высот, то образуется треугольник, подобный данному)⇒
∆ А1В1С подобен ∆ АВС.
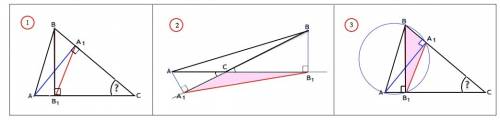
Случай 1)
∆ АВС остроугольный. Из подобия треугольников следует отношение:
А1B1:АB=В1С:ВС=cosC
cosC= 2√3:4=√3/2 ⇒ угол С=30°
2)
∆АВС тупоугольный и угол С >90°:
по первой лемме о высотах ∆ А1В1С подобен ∆ АВС.
Косинус угла, смежного с углом С, равен
А1С:АС=В1С:ВС=cos ACA1
cos ACA1=А1В1:АВ=2√3:4=√3/2, угол АСА1=30°, ⇒
угол С=180°-30°=150°
Таким же образом находится величина острого угла С в тупоугольном ∆ АВС, где тупой угол – ∠А или ∠В.
————————————
3) Можно угол С найти по т.синусов.
Так как. ∆АВВ1 и АА1В1 прямоугольные с общей гипотенузой АВ, можно провести окружность около четырехугольника АВА1В1. Треугольник АВВ1 - вписанный.
По т. синусов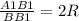 
2R=AB=4 ⇒
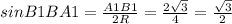. Это синус 60°, и тогда
угол С=30°.
Этот решения применим и в случае тупоугольного ∆ АВС.
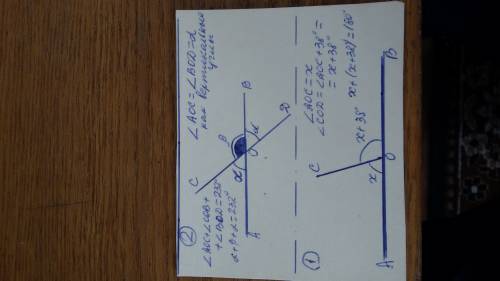
Видимо в недописанном условии: 270<a<360.
Значит косинус положителен.
cosa = кор(1-sin^2 a) = кор(1-0,64) = 0,6
(Если же угол а: 180<a<270, то ответ: -0,6)