∠А = 13°. ∠Ч = 150,7°. ∠Т = 16,3°.
Объяснение:
Железнодорожная линия между городами образует треугольник АЧТ, где А - Алматы, Ч - Чу и Т -Тараз. Углы поворотов при этих городах найдем по теореме косинусов.
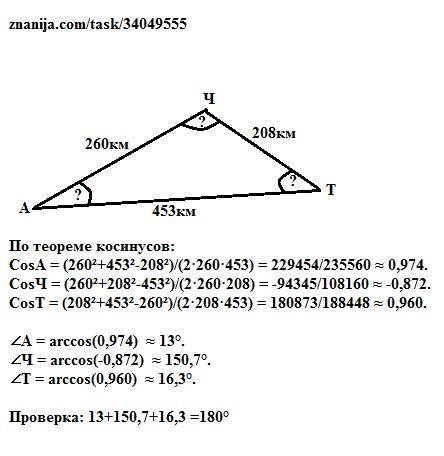
По теореме косинусов:
СosA = (260²+453²-208²)/(2·260·453) = 229454/235560 ≈ 0,974.
СosЧ = (260²+208²-453²)/(2·260·208) = -94345/108160 ≈ -0,872.
СosТ = (208²+453²-260²)/(2·208·453) = 180873/188448 ≈ 0,960.
∠А = arccos(0,974) ≈ 13°.
∠Ч = arccos(-0,872) ≈ 150,7°.
∠Т = arccos(0,960) ≈ 16,3°.
Проверка: 13+150,7+16,3 =180°
Дана правильная четырехугольная пирамида SАВСД, длина бокового ребра которой равна L = 3 см, а стороны основания a = 2√3 см.
Проведём осевое сечение через 2 боковых ребра.
В сечении равнобедренный треугольник АSС с боковыми сторонами L = 3 см и основанием - диагональ квадрата основания d = a√2 = (2√3)*√3 = 2√6 см.
Высота Н пирамиды равна:
Н = √(L² - (d/2)²) = √(9 - 6) = √3 см.
Перпендикуляр из центра основания пирамиды на боковое ребро (пусть это ОК) - это высота треугольника ОSС, она равна (√3*√6)/3 = √2 см.
Искомый угол лежит в перпендикулярном сечении к боковому ребру.
В сечении - треугольник ВКД.
Апофема А = √(3² - (2√3/2)²) = √(9 - 6) = √3 см.
КД - высота, она равна 2S/L = (2*((1/2)*2√3*√6))/3 = 2√2 см.
То есть она как гипотенуза треугольника ОКД в 2 раза больше катета ОК, а угол КДО равен 30 градусов.
Отсюда искомый угол ВКД равен 2*60 = 120 градусов.
задача то простая
..................................