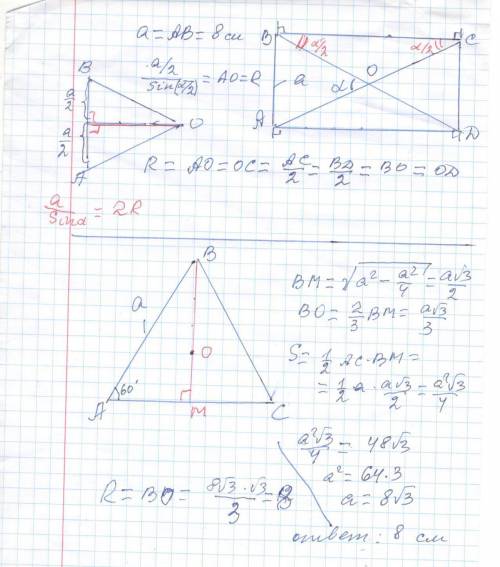
Найдите длину окружности , описанной около:
1)прямоугольника, меньшая сторона которого равна 8 см, а угол между диагоналями равен α;
2)правильного треугольника, площадь которого равна 48√3 см²
1) R = AC/2 * * * R =d/2 = AC/2 =AO * * *
Из ΔABC: AC =2*AO =AB /sin(α/2) =8/sin(α/2)
R = 4/sin(α/2)
2) a/sinα =2R ⇒ R = a/2sinα =a/2sin60° =a/(2*√3 /2) = a /√3 || (a√3)/3 ||
* * * S = (1/2)*absinC * * * S = (1/2)*a*a*sin60° =(a²√3) / 4
48√3 =(a²√3) / 4 ⇔a²/ 4 = 48 ⇔a² =4*48 = 4*16*3 ⇒ a=8√3
R = a /√3 = 8√3/√3 =8
1) Данный треугольник - вписанный.
Тогда АС - диаметр окружности, и треугольник АВС - прямоугольный с прямым углов при вершине В, т.к. угол, опирающийся на диаметр, равен 90°.
Если угол А=30, то угол С=90°-30°=60° ( из суммы острых углов прямоугольного треугольника)
2) Треугольник не вписан в окружность, просто АС проходит через её центр. . Тогда, даже если АС равна диаметру, задача не имеет решения, так как сумма углов В и С будет 180°-30°=150° градусов, но величина их может быть любой. (см. рисунок)------
Интересно, что задач с подобным условием много (только градусная мера угла разная), и нигде не отмечено, что данный треугольник - вписанный.