
Объяснение:
координаты вектора вычисляются так: из соответствующей координаты конца вектора нужно вычесть соответствующую координату начала вектора.
получим координаты вершин параллелограмма, выраженные через координаты одной точки (точки А, например)
координаты векторов-диагоналей параллелограмма вычисляются аналогично...
косинус угла между векторами = частному от деления скалярного произведения векторов на произведение длин векторов.
скалярное произведение векторов=сумме произведений соответствующих координат.
длина вектора=корню квадратному из суммы квадратов координат (т.Пифагора)
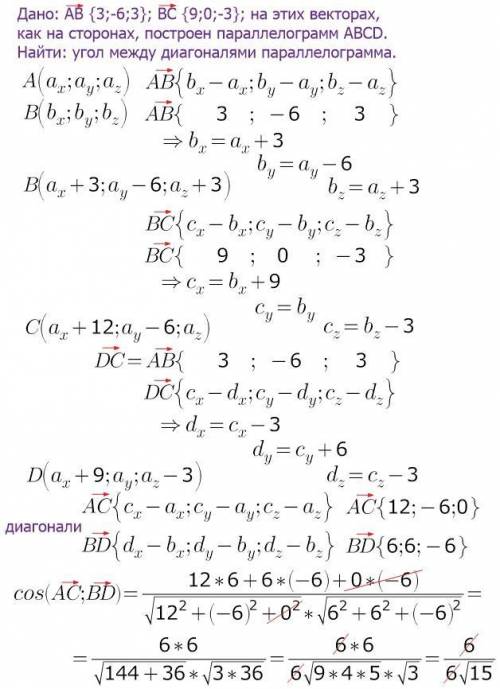
ответ:
объяснение:
1) давайте разберемся, что такое смежные углы
представьте, что идет снег, и мы сидим в машине.
теперь включим стеклоочиститель - или дворник (лобовой стекло у нас большое, а дворник всего один, но он легко ходит от одного конца до другого ) так что на окне у нас образовался полукруг (чистое стекло без снега). вот вы выключили дворник, и он застыл на одном месте. и вот этот дворник уже и образует два смежных угла. с одной стороны острый, а с другой тупой. на рисунке ав - прямая- 180 градусов, ое - это дворник, угол аое - острый , еов - тупой; вот и все
2) вам нужен смежный угол аос, сд будет прямая, оа - дворник, а смежный угол аод. вот когда будете думать про смежный угол, вспомните снежок и дворник
3) а теперь дайвате разберемся с вертикальными углами.
с нами в машине сидит нарядный джентельмен с бабочкой на шее.
его бабочка уже образовала две пары вертикальных углов. на вашем рисунке тоже есть такая бабочка, она образовалась при пересечении двух прямых ав и сд, ∠аос=∠ доб , а ∠аод=∠соб, и тут бабочка взлетает вертикально вверх!
4) если все хорошенько представили, то ответить на два вопроса и трудности не будет!
Для начала уточним, что если один угол ромба равен 60°. то второй равен 120°, а не 110°, т.к. сумма углов, прилегающих к одной стороне параллелограмма ( а ромб - параллелограмм), равна 180°.
Определение:
Две прямые в трехмерном пространстве называются скрещивающимися, если они не лежат в одной плоскости, не пересекаются, не параллельны и не совпадают, иначе они лежали бы в одной плоскости.
Поскольку m параллельна МР, она не параллельна NР и не лежит с ней в одной плоскости, т.к. МР и MN пересекаются.
Прямые m и NP - скрещивающиеся прямые.
Решение задачи по нахождению величины угла между скрещивающимися прямыми в принципе такое же, как при решении задачи по определению угла между пересекающимися прямыми.
То есть угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, соответственно параллельными данным.
Проекция прямой m на плоскость ромба параллельна m и параллельна МР. Она пересекается со стороной робма MN под тем же углом, под каким пересекается с этой стороной диагональ МР.
Угол между проекцией m на плоскость ромба и его стороной NP равен половине тупого угла ромба, т.к. МР, как диагональ ромба, делит угол 120 градусов пополам. (Диагонали ромба - биссектрисы его углов).
Итак, прямые m и MN скрещивающиеся и угол между ними равен 60 градусов.