Чертеж к решению - во вложении.
Известно, что биссектрисы двух непротивоположных углов параллелограмма пересекаются под прямым углом и отсекают равнобедренные треугольники. Таким, образом, треугольники АВК и МСД равнобедренные, а треугольник КРМ - прямоугольный.
Все равные углы (накрест лежащие и вертикальные), а также равные отрезки отмечены на чертеже.
Ведем обозначения: ВК=КМ=МС=х, КР=у, МР=z.
Периметр параллелограмма P=2(АВ+ВС)=8х.
Треугольники РАД и РКМ подобны по двум углам. Поэтому
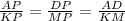
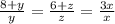
1) 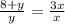
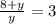
3y=8+y
y=4,
2) 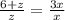
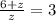
z+6=3z
z=3,
По теореме Пифагора в треугольнике КРМ
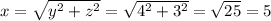
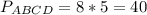
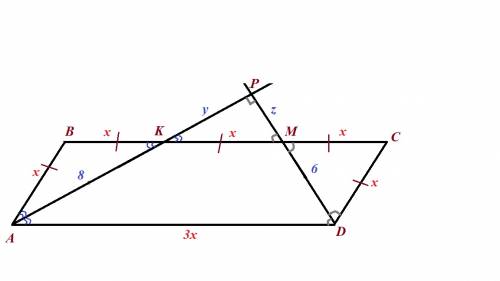
ответ: 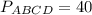
1) узнаем сколько всего частей 3+2=5
2) т.к. это прямоугольник то уго углы прямые, т.к. равны 90 градусам.
3) 90/5=16 приходится на одну часть
4) 16*2=32
5) 16*3=48
проведём две диагонали. Одна из них пусть будет АС , а другая ВР
Точка О-пересение диагоналей.
т.к. это прямоугольник, то треугольник ВОА-равнобедренный, углы при основании равны.
значит угол ВОА=180-2*32=116 (он тупой, тк. больше 90)
Тогда рассмотрим треугольник АОР-также равнобедренный. углы при основании равны. значит угол АОР=180-2*48=84 (он острый, т.к. меньше 90)
ответ: 84
Не забудьте поблагодарить