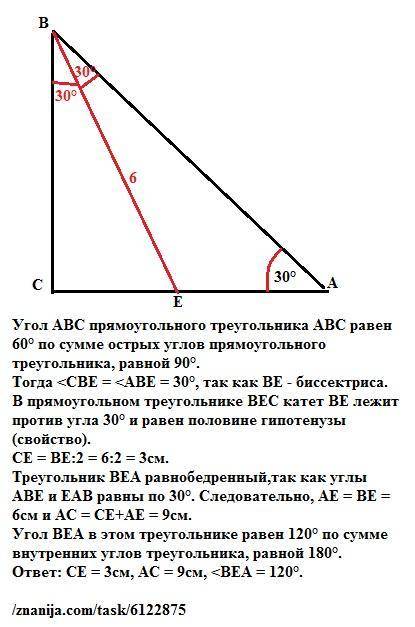
Угол АВС прямоугольного треугольника АВС равен 60° по сумме острых углов прямоугольного треугольника, равной 90°.
Тогда <CBE = <ABE = 30°, так как ВЕ - биссектриса. В прямоугольном треугольнике ВЕС катет ВЕ лежит против угла 30° и равен половине гипотенузы (свойство).
СЕ = ВЕ:2 = 6:2 = 3см.
Треугольник ВЕА равнобедренный,так как углы АВЕ и ЕАВ равны по 30°. Следовательно, АЕ = ВЕ =6см и АС = СЕ+АЕ = 9см.
Угол ВЕА в этом треугольнике равен 120° по сумме внутренних углов треугольника, равной 180°.
ответ: СЕ = 3см, АС = 9см, <BEA = 120°.
угА + угВ + угС + угД = 360 гр
Пусть х - угА, тогда согласно условию уг.В - 3,5х
Составим и решим уравнение:
2х + 7х = 360
9х = 360
х = 40
два угла по 40 гр. и два угла по 140 гр.