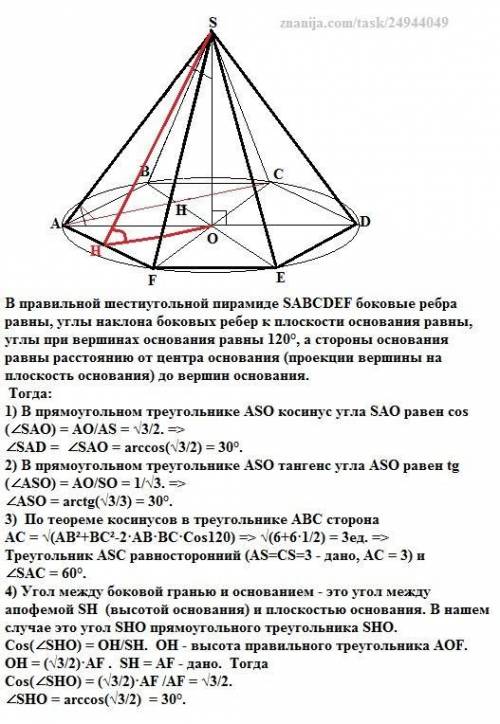
1) ∠SAD = 30°.
2) ∠ASO = 30°.
3) ∠SAC = 60°.
4) ∠SHO = 30°.
Объяснение:
В правильной шестиугольной пирамиде SABCDEF боковые ребра равны, углы наклона боковых ребер к плоскости основания равны, углы при вершинах основания равны 120°, а стороны основания равны расстоянию от центра основания (проекции вершины на плоскость основания) до вершин основания.
Тогда:
1) В прямоугольном треугольнике АSО косинус угла SAO равен сos(∠SAO) = АО/AS = √3/2. =>
∠SAD = ∠SAO = arccos(√3/2) = 30°.
2) В прямоугольном треугольнике АSО тангенс угла АSO равен tg(∠ASO) = АО/SO = 1/√3. =>
∠ASO = arctg(√3/3) = 30°.
3) По теореме косинусов в треугольнике АВС сторона
АС = √(АВ²+ВС²-2·АВ·ВС·Cos120) => √(6+6·1/2) = 3ед. =>
Треугольник АSС равносторонний (AS=CS=3 - дано, АС = 3) и
∠SAC = 60°.
4) Угол между боковой гранью и основанием - это угол между апофемой SH (высотой основания) и плоскостью основания. В нашем случае это угол SHO прямоугольного треугольника SHO.
Cos(∠SHO) = OH/SH. OH - высота правильного треугольника AOF.
OH = (√3/2)·AF . SH = AF - дано. Тогда
Cos(∠SHO) = (√3/2)·AF /AF = √3/2.
∠SHO = arccos(√3/2) = 30°.
Объяснение:
1. Вершины многоугольника называются соседними, если они являются концами одной из его сторон.Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
3. Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
4. Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).
5. Ромб - четырехугольник-параллелограмм, у которого противоположные стороны равны.
6. 1) Имеет все свойства параллелограмма
2) Диагонали перпендикулярны
3) Диагонали являются биссектрисами его углов
4) Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре
5) Точка пересечения диагоналей называется центром симметрии ромба
6) В любой ромб можно вписать окружность.
7) Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
8. Да, т. к. он лежит по одну сторону от всех прямых, проходящих через его вершины
9. 1) Диагонали параллелограмма точкой своего пересечения делятся пополам.
2) Любая диагональ делит параллелограмм на два одинаковых треугольника.
3) Сумма квадратов диагоналей параллелограмма равна двойной сумме квадратов его двух смежных сторон.
4) Площадь параллелограмма равна произведению длин диагоналей помноженных на синус угла между ними.
10. Есть 3 признака параллелограмма,возьми и загугли)) там даже буду с формулами.
11. четырехугольник, у которого только одна пара противолежащих сторон параллельна . Параллельные стороны называются-основаниями трапеции. Две другие стороны называются-боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется-средней линией трапеции
12.
— равнобедренные трапеции;
— прямоугольные трапеции;
— произвольные трапеции.
ДАЛЬШЕ ПИШИ САМ ВСЁ ЕСТЬ В ИНТЕРНЕТЕ И В КНИЖКЕ,ЛЕНТЯЙ!