ответ: 432π
Объяснение: обозначим радиус r, a высоту h. Если r/h=1/2, то: h=2r. 2 радиуса
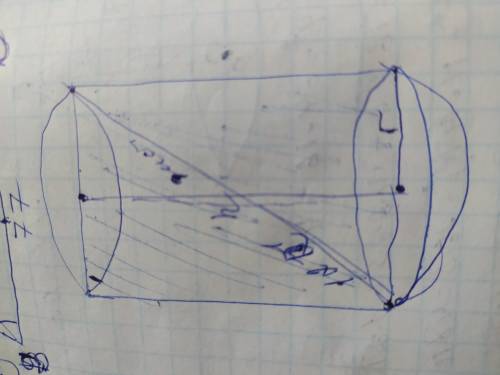
- это диаметр, и диаметр основания равен высоте. Высота, радиус и диагональ осевого сечения цилиндра образуют равнобедренный прямоугольный треугольник, в котором диаметр основания и высота являются катетами а диагональ гипотенузой. В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому h=диаметру=12√2/√2=
=12, тогда радиус=12/2=6
Найдём площадь основания по формуле:
Sосн=πr²=π×6²=36π
Теперь найдём объем цилиндра зная его площадь основания и высоту по формуле: V=Sосн×h=36π×12=432π(ед³)
6х+9х=360
15х=360
х=24
Меньшая дуга АВ равна 6*24=144°.
Рассмотрим треугольник АВС. Он прямоугольный, т.к. вписанный угол В опирается на диаметр (вписанный угол, опирающийся на полуокружность - прямой).
Сумма острых углов прямоугольного треугольника равна 90°. Рассмотрим эти углы.
Угол С - вписанный, опирающийся на меньшую дугу АВ, равную 144°. Значит, он равен ее половине:
<C=1/2*144=72°
<A=90-<C=90-72=18°