40°,40°,140°,140°
Объяснение:
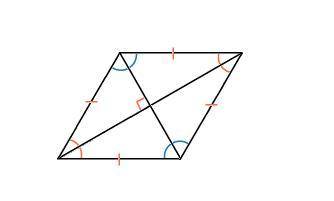
Свойства ромба:
Диагонали ромба перпендикулярны., т.е пересекаются под углом 90°
Диагонали ромба делят его углы пополам.
диагонали делят параллелограмм на четыре равных прямоугольных треугольника
Исходя из этого, рассмотрим один из треугольников
Сумма всех углов треугольника = 180°.
Один их углов равен 90°,
второй угол будет равен 2х
третий угол 7х
( по условию), тогда
2х+7х+90=180
9х=90
х=90:9
х=10
значит углы треугольника равны
2*10=20°
7*10=70°
поскольку диагонали ромба делят его углы пополам . Значит получаем, что у ромба такие углы:
20*2=40°
70*2=140°
У ромба противоположные углы равны, значит углы ромба равны 40,40,140,140 градусов
Пусть х - меньшая диагональ ромба, тогда х+4 - большая диагональ.
диагонали ромба взаимно перпендикулярны, в точке пересечения делятся пополам, используя теорему Пифагора
составляем уравнение:
(x/2)^2+((x+4)/2)^2=10^2;
x^2+x^2+8x+16=400;
2x^2+8x-384=0;
x^2+4x-192=0;
D=784=28^2
x1=(-4-28)/2<0 - не подходит
x2=(-4+28)/2=12
х=12
х+4=12+4=16
Площаль ромба равна половине произведения диагоналей,
S=12*16/2=96 кв.см