Объяснение:
1. Теорема: сумма угловΔ-ка = 180°. Из этого следует:
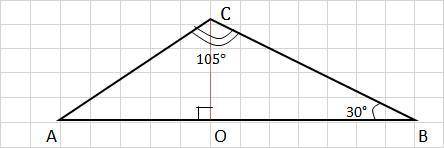
∠А = 180° - 30° -105° = 45° → ∠А = 45°
2. Из ∠С построим высоту СО:
СО⊥ АВ.
Рассмотрим ΔАОС.
∠АОС = 90° по построению,
∠А = 45°, значит, ∠АСО =90°- 45° = 45°.
Следовательно, ΔАОС - равнобедренный и
АО=СО.
По т. Пифагора:
АС² = АО² + СО² → АС² = 2СО² или
4² = 2*СО²
СО² = 16/2 = 8 → СО = √8 = 2√2.
СО = АО = 2√2
3. Рассмотрим ΔСОВ.
∠СОВ = 90° по построению
∠В = 30°
СО = 2√2 - катет, лежащий против угла в 30°.
Теорема: В прямоугольном Δ - ке против угла в 30° лежит катет, равный половине гипотенузы:
СВ = 2СО= 2 * 2√2 = 4√2
ОВ² =СВ² - СО² = (4√2)² - (2√2)² = 32 - 8 = 24
ОВ = √24 = 2√6
АВ = АО + ОВ = 2√2 +2√6
∠А = 45°
СВ = 4√2 ≈ 4* 1,41 = 5,64(см0
АВ = 2√2 +2√6 = 2* 1,41 +2*2,45 = 2,82 + 4,9 = 7,72 (см)
Объяснение:
Так как BС=СD по условию, то ∆BCD – равнобедренный с основанием BD. Следовательно угол СВD=угол CDB как углы при основании равнобедренного треугольника.
Сумма углов любого треугольника равна 180°.
Исходя из этого угол ВСD=180°–угол CBD–угол СDB=180°–x–x=180°–2x
Пусть угол СВD=x, тогда угол CDB=х так же.
Основания трапеции параллельны, тоесть ВС//AD.
Тогда угол CBD=угол ADB как накрест лежащие при параллельных прямых ВС и AD и секущей BD.
Так как СВD=x, то угол ADB=x так же.
Так как BD=AD по условию, то ∆АВD – равнобедренный с основанием АВ. А углы при основании равнобедренного треугольника равны. Сумма углов в любом треугольнике равна 180°.
Исходя из этого: угол ABD=(180°–угол ADB)÷2=(180°–x)÷2
Угол АВС=угол ABD+угол CBD=(180°–x)÷2+x
Так как АВ=CD по условию, то трапеция ABCD – равнобедренная.
Углы при основании равнобедренной трапеции равны, тоесть: угол АВС=угол BCD.
Подставим величины этих углов, получим уравнение:
(180–x)÷2+x=180–2x
90–0,5х+х=180–2х
–0,5х+х+2х=180–90
2,5х=90
х=36
Тогда угол ВСD=180°–2*36°=108°
ответ: 108°