.(Точка s віддалена від площини трикутника abc на 3 см, і рівновіддалена від його сторін, які дорівнюють 13,14,15см. знайти відстані від точки s до сторін трикутника.).
S - данная точка.SO = 3. Если S равноудалена от сторон треугольника, то точка О - центр вписанной окружности для тр. АВС. Найдем радиус r вписанной окр-ти, воспользовавшись формулами для площади тр-ка:
S = p*r
S = = 84
Где р = (a+b+c)/2 = (13+14+15)/2 = 21 - полупериметр.
Находим r:
r = S/p = 84/21 = 4.
Проведем перпендикуляр SK из S на сторону, например, ВС. В пр. тр-ке SKO:
АВ = Рabcd : 4 = 12 : 4 = 3 см ВВ₁ и DD₁ - медианы, значит AD₁ = D₁B = AB₁ = B₁D = 3/2 см
ΔABD равнобедренный, поэтому ∠ABD = ∠ADB, BD₁ = DB₁, BD - общая сторона для ΔDD₁B и ΔBB₁D, значит эти треугольники равны по двум сторонам и углу между ними, ⇒ BB₁ = DD₁.
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины. Обозначим OD₁ = OB₁ = x, тогда OD = OB = 2x. ΔOBD равнобедренный, значит ∠OBD = ∠ODB = 40°. ∠D₁OB = ∠OBD + ∠ODB = 80° как внешний угол ΔDOB.
Если необходимо числовое значение, а не выражение, можно взять значение cos 80° по таблице, тогда получится: cos 80° ≈ 0,1736 BB₁ = 9 / (2√(5 - 4cos80°)) ≈ 2,2
Так как призма прямая и в основании квадрат, все углы между ребрами прямые. Между пересекающимися боковым ребром и диагональю основания, а так же пересекающимися стороной основания и диагональю боковой грани уголы прямые (если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости, проходящей через точку пересечения). По теореме Пифагора находим: (17^2-15^2)=64 - квадрат диагонали основания. 64/2 = 32 - квадрат стороны основания. 32 + 15^2 = 32+225 =257 - квадрат диагонали боковой грани \|257 (см) - диагональ боковой грани
S - данная точка.SO = 3. Если S равноудалена от сторон треугольника, то точка О - центр вписанной окружности для тр. АВС. Найдем радиус r вписанной окр-ти, воспользовавшись формулами для площади тр-ка:
S = p*r
S =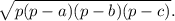 = 84
= 84
Где р = (a+b+c)/2 = (13+14+15)/2 = 21 - полупериметр.
Находим r:
r = S/p = 84/21 = 4.
Проведем перпендикуляр SK из S на сторону, например, ВС. В пр. тр-ке SKO:
КО = 4, SO = 3
Тогда искомое расстояние SK = кор(16+9) = 5.
ответ: 5 см.