:
: (0;1)_ ответ
(0;1)_ ответ
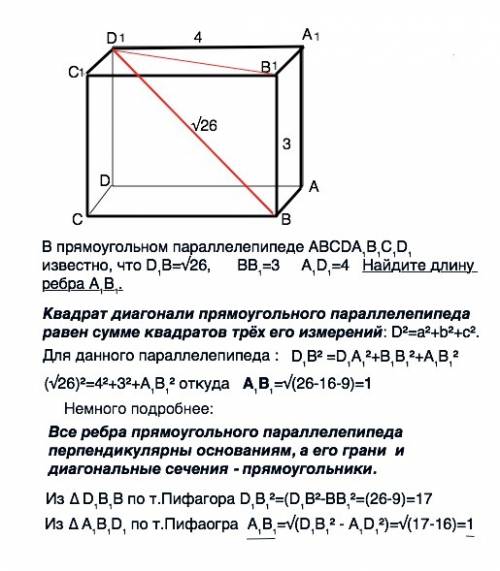
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
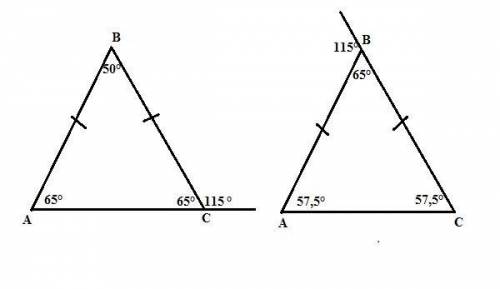
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что D₁B=√26, BB₁=3 A₁D₁=4 Найдите длину ребра A₁B₁.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
D²=a²+b²+c². Для данного параллелепипеда :
D₁B² =D₁A₁²+B₁B₁²+A₁B₁²
(√26)²=4²+3²+A₁B₁² откуда
А₁В₁=√(26-16-9)=1
-------------------
Если забыли данную выше формулу, т.Пифагора наверняка все помнят.
Все ребра прямоугольного параллелепипеда перпендикулярны основаниям, а его грани и диагональные сечения - прямоугольники.
Из ∆ D₁B₁B по т.Пифагора D₁B₁²=(D₁B²-BB₁²=(26-9)=17
Из ∆ A₁B₁D₁ по т.Пифаогра А₁В₁=√(D₁B₁² - A₁D₁²)=√(17-16)=1