ответ: S=9см²
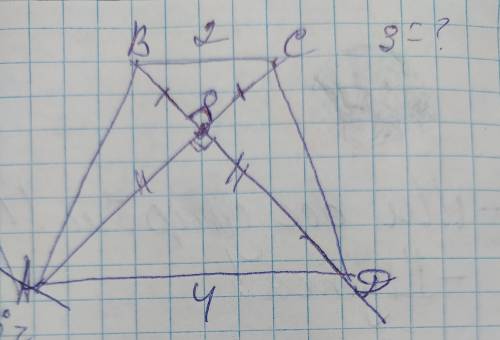
Объяснение: площадь трапеции с диагоналями пересекающимися под прямым углом вычисляется по формуле:
S=d²/2
Так как трапеция равнобедренная, то АВ=СД, и диагонали АС=ВД и при пересечении они делятся на одинаковые отрезки. Найдём величину диагонали. Диагонали АС и ВД образуют при пересечении 2 равнобедренных прямоугольных треугольника ВОС и АОД, в которых ВО=СО и АО=ДО , которые являются катетами, а ВС и АД - гипотенузы. Катет равнобедренного прямоугольного треугольника меньше гипотенузы в √2 раз, поэтому ВО=СО=2/√2см, а
АО=ДО=4/√2см.
Тогда АС=ВД=4/√2+2/√2=6/√2
Теперь найдём площадь трапеции зная её диагонали:
S=(6/√2)²÷2=36÷2÷2=9см²
Рисуем треугольник АВС, где АС = 24 см и АВ = ВС. Проводим высоту ВК = 9 см
Площадь треугольника,
S = 24 * 9 / 2 = 108 кв.см
По свойствам равнобедренного треугольника
АК = КС = АС / 2 = 24 / 2 = 12 см
По теореме ПИфагора
АВ^2 = ВК^2 + AK^2 = 9^2 + 12^2 = 81 + 144 = 225 = 15^2
АВ = 15 см
Полупериметр
р = (АВ + ВС + АС) / 2 = (15 + 15 + 24) / 2 = 27 см
Радиус вписанной окружности
r = S / p = 108 / 27 = 4 см
Синус угла А = ВК / АВ = 9 / 15 = 0,6
Радиус описанной окружности
R = ВС / (2 * синус А) = 15 / (2*0,6) = 12,5 см