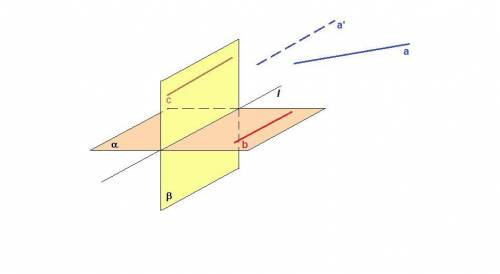
Предположим, что прямая а не пересекает плоскости α и β.
Значит, прямая а параллельна обеим плоскостям.
Тогда в каждой плоскости найдется прямая, параллельная прямой а. Пусть это прямые b и с.
Так как b║a и с║а, то b║c.
Если прямая с параллельна прямой b, лежащей в плоскости α, то с║α.
Плоскость β проходит через прямую с, параллельную плоскости α, и пересекает плоскость α, значит линия пересечения плоскостей параллельна прямой с.
Итак, c║l, c║a, ⇒ l║a. Но прямые l и а скрещивающиеся. Получили противоречие.
Значит, прямая а пересекает хотя бы одну из плоскостей.
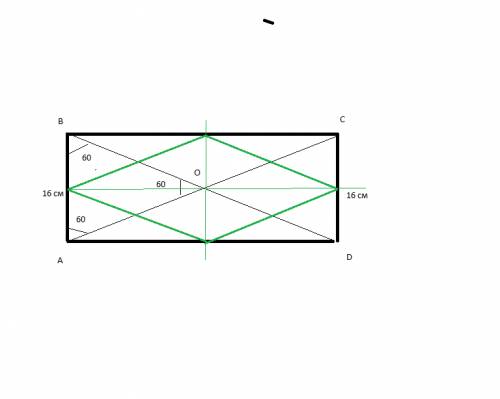
сделаем построение - сразу все видно
точки K L M N - середины сторон прямоугольника АВСД
проведем прямые LN (параллельна АВ и СД) и КМ (параллельна ВС и АД)-
они образуют равные прямоугольники (стороны попарно равны)
KBLO с диагональю KL
OLCM с диагональю LM
NOMD с диагональю NM
АKОN с диагональю KN
и так понятно, что диагонали в равных прямоугольниках равны
KL=LM=NM=KN
но если кто сомневается , то можно доказать через теорему Пифагора
KL^2=KB^2+BL^2
LM^2=LC^2+CM^2
NM^2=MD^2+ND^2
KN^2=AN^2+AK^2
правые части этих выражений равны - это все половинки сторон
а значит равны и левые части
итак все стороны нового четырехугольника равны - это основное свойство РОМБА
если бы начальной фигурой был квадрат - то внутри тоже получился бы квадрат - но у нашего ромба углы 60-120-60-120
ответ: 112 и 109