Пересечение 6 -2.
Объяснение:
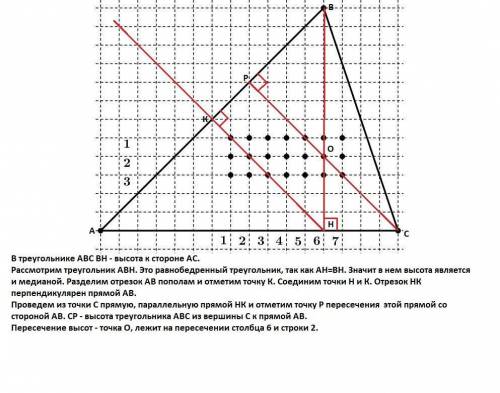
В треугольнике АВС ВН - высота к стороне АС.
Рассмотрим треугольник АВН. Это равнобедренный треугольник, так как АН=ВН. Значит в нем высота является и медианой. Разделим отрезок АВ пополам и отметим точку К. Соединим точки Н и К. Отрезок НК перпендикулярен прямой АВ.
Проведем из точки С прямую, параллельную прямой НК и отметим точку Р пересечения этой прямой со стороной АВ. СР - высота треугольника АВС из вершины С к прямой АВ.
Пересечение высот - точка О, лежит на пересечении
столбца 6 и строки 2.
Отрезок AD=DE (по условию)
Угол АDB=углу EDC (накрест лежащие)/
Следовательно треугольники ABD и ECD равны по двум сторонам и углу между ними.
Угол ACE равен сумме углов ACD и DCE.
Угол ACD = 56 градусов (по условию)
Угол DCE=углу DBA (т.к. треугольник ABD равен треугольнику DEC)
56+40=96 градусов.