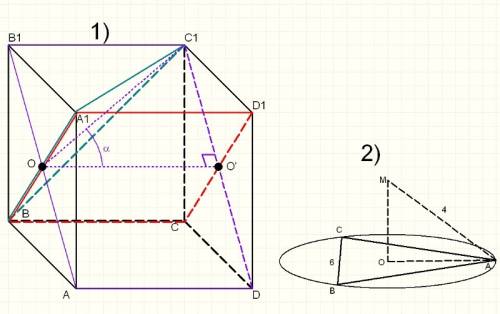
1) основание пирамиды прямоугольный треугольник acb, где ac=6 и sina=0,8. все боковые рёбра наклонены к плоскости основания под углом 60 градусов. найти объём пирамиды. 2) основанием пирамиды служит ромб со стороной равной 25 см и меньшей диагональю равной 30 см. все боковые грани пирамиды равнонаклонены к основанию. площадь сечения, проведенного через большую диагональ основания и вершину пирамиды, равна 80 см в квадрате. найдите площадь боковой поверхности пирамиды.
Пусть С - начало координат
Ось X - CB
Ось Y - Перпендикулярно X в сторону A
Ось Z - СС1
1)
Координаты точек
D (√13;0;√13/2)
N(3√13/4;√39/4;√13)
Вектора
СD ( √13;0;√13/2)
DN( -√13/4;√39/4;√13/2)
CD*DN = -13/4 + 13/4 =0 - перпендикулярны.
2)
Уравнение плоскости
BCC1
y=0
Уравнение плоскости
CDN
ax+by+cz=0
подставляем координаты точек D и N
√13a + √13c/2 =0
3√13a/4 + √39b/4 + √13c =0
Пусть a=1 тогда с = -2 b= 5√3/3
Уравнение
x +5√3y/3 - 2z =0
Косинус искомого угла
5√3/3 / √(1+25/3+4) = √(5/8)
Синус √(3/8)
Тангенс √(3/5)= √15/5