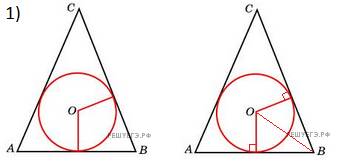
1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение.
Треугольники HOBи KOB равны, т. к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=3
PABC=AC+CB+AH+HB=2CB+2HB=16+6=22
ответ: 22
2. В равнобедренный треугольник АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите радиус окружности, если АМ = 8 и ВМ = 12.
S=1/2p*r
r=2s/p
Т.к треугольник ABC-равнобедренный, то AB=AC=30
По свойству касательных: АМ=АЕ=8, СЕ=СК=12,ВМ=КВ=12,значит ВС=24
По формуле Герона S треугольник = в корне p(p-a)(p-b)(p-c)
Объяснение:
1
<EBC=180°-<C-<BEC=180°-90°-60°=30°,EB=EC*2=5*2=10 см
<BEC=<AEC-<BEC=180°-60°=120°,
<ABE=180°-<BEC-<BAE=180°-120°-30°=30°,значит
ΔAEB-равнобедренный,AE=EB=10 см
AC=AE+EC=10+5=15 см
2
ΔАСВ-РАВНОБЕДРЕННЫЙ прямоугольный,так как углы при основании 45°.CD-высота,биссектриса и медиана.Значит ΔCDB ,ΔACD-тоже равнобедренныe прямоугольныe, CD=DB=AD=8 см
AB=2AD=2*8=16 см
3
<ACD=<АCЕ-<DCE=45°-20°=25° <A=180°-<ACD-<ADC = =180°-90°-25°=65°
<B=180°-<ACВ-<СAВ= 180°-90°-6 5°=25°
прости не знаю? ему