Пусть координаты центра равны (a; b), а длина отрезка АВ равна R
Тогда уравнение примет вид
(x-a)^2 + (y-b)^2 = R^2
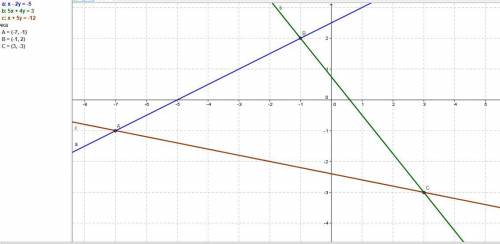
Даны уравнения прямых, проходящих через стороны треугольника ABC:
AB : x – 2y + 5 = 0
BC : 5x + 4y – 3 = 0
AC : x + 5y + 12 = 0.
Пересечение прямых АВ и ВС (точка В - общая) даёт точку В.
AB : x – 2y + 5 = 0 х2 = 2x - 4y + 10 = 0
BC : 5x + 4y – 3 = 0 5x + 4y - 3 = 0
7x + 7 = 0, x = -7/7 = -1, y = (x + 5)/2 = 2.
Точка В(-1; 2).
Аналогично определяем точку А.
AC : x + 5y + 12 = 0.
AB : x – 2y + 5 = 0 вычитаем
7y + 7 = 0, y = -7/7 = -1, x = 2y - 5 = -7.
Точка А(-7; -1).
Определяем точку С.
BC : 5x + 4y – 3 = 0 5x + 4y - 3 = 0
AC : x + 5y + 12 = 0. х(-5) = -5x - 25y - 60 = 0
-21y - 63 = 0. y = -63/21 = -3, x = -5x - 12 = 3.
Точка С(3; -3).
общая y=(x-a)²+(y-b)²=R²