В объяснении.
Объяснение:
1. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+3х+4х = 360° => х = 36°.
Больший угол равен 4х = 144°.
2. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+2х+4х = 360° => х = 40°.
Меньший угол равен 4х = 40°.
3. Площадь квадрата равна площади прямоугольника: 4*9 = 36 =>
Сторона квадрата равна √36 = 6 ед.
4. Площадь прямоугольника равна х*(х+2) = 24. Тогда
х² + 2х - 24 = 0. Решаем квадратное уравнение. => x = 6. (второй корень отрицательный)
Тогда большая сторона равна 6 + 2 = 8 ед.
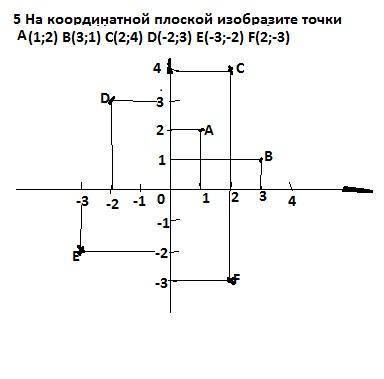
5. Смотри рисунок.
6. Уравнение окружности:
(Х - Хц)² + (Y-Yц)² = R² Тогда
а) Координаты центра: Ц(-5;2) Радиус = 4 ед.
б) Координаты центра: Ц(0;-3) Радиус = 3 ед.
1)Сумма внешних углов не зависит от n и равна 2π. Следовательно внешний угол правильного девятиугольника равен 360°:9=40°
2)формула суммы внутренних углов выпуклого мн-ка 180*(н-2), где н число сторон
решается уравнение: 2520=180(н-2) 18н-36 =252 18н=252+36 н=(252+36):18
3)Раз все углы одинаковы - то и все стороны одинаковы, значит многоугольник правильный.
Угол правильного мн-ника рассчитывается по интересной формуле Alpha = (180*n - 360) / n = 180 - 360 / n Здесь n - это количество сторон, которое нам надо узнать 135 = 180 - 360/n 360/n = 180 - 135 = 45 n = 360/45 = 8
4)
пусть (х) см приходится на 1 часть, тогда (7х) см-1 сторона (меньшая) (8х) см-2 сторона (9х) см-3сторона (10х) см-4 сторона. Зная, что периметр равен 68 см, составим и решим уравнение: 7х+8х+9х+10х=6834х=68х=22см проходится на 1 часть2*7=14(см) -меньшая сторонаответ: 14сиответ: 14 см
3)7*2=14 см - меньшая сторона
5)УсловиеВ выпуклом четырехугольнике ABCD отрезок, соединяющий середины сторон AB и CD равен 1. Прямые BC и AD перпендикулярны. Найдите отрезок, соединяющий середины диагоналей AC и BD. Скрыть с вершинами в серединах AB, AC, CB и BD - прямоугольник. РешениеПусть K и M - середины сторон соответственно AB и CD четырехугольника ABCD, а N и L - середины его диагоналей соответственно AC и BD. Тогда KLMN - параллелограмм, а т. к. KN || BC, KL || AD и BC AD, то он - прямоугольник. Следовательно, NL = KM = 1. ответ1.
6)В выпуклом многоугольнике сумма дополнений углов до развернутого равна 360°. В данном случае для первых пяти углов она равна 40 * 5 = 200°. Остается 160°. Это число нельзя представить даже в виде двух слагаемых, каждое из которых > 90° (если остальные углы острые, то дополнительные >90°). Поэтому к пяти имеющимся углам можно добавить только один. а данный многоугольник - шестиугольник
Объяснение:
1.
а) Так как даны концы диаметра, то, для нахождения центра окружности, нам нужно найти координаты середины диаметра.
х₀=(х₁+х₂)/2=(-1+5)/2=2
у₀=(у₁+у₂)/2=(5-5)/2=0
Координаты центра окружности О(2;0).
б) Для составления формулы окружности найдем её радиус.
R=√((x₁-x₀)² + (y₁-y₀)²)=√(9+25)=√36=6
Значит уравнение окружности имеет вид:
(х-2)²+(у-0)²=6² ⇔
(х-2)²+у²=36
2.
а) В параллелограмме диагонали точкой пересечения делятся пополам. Поэтому достаточно найти середину одной из диагоналей. чтобы найти точку их пересечения. Найдем середину ВД:
х₀=(х₁+х₂)/2=(-3+2)/2= -0,5
у₀=(у₁+у₂)/2=(-1+3)/2=1
Координаты точки пересечения диагоналей О(-0,5;1)
б) У параллелограмма ABCD стороны АВ║СД и ВС║ДА. Найдем вектор АВ: (-3-1;-1+2)=(-4;1).
Для параллельных прямых направляющие векторы совпадают. При этом вектор АВ совпадает с вектором ДС (а не СД!)
Найдем координаты точки С по точке Д и направляющему вектору
С(2+(-4);3+1) ⇔ С(-2;4)
в) ДЛя нахождения периметра найдем длины АВ и ВС и умножим их сумму на 2.
Длина АВ=√((x₂-x₁)² + (y₂-y₁)²)=√((-3-1)² + (-1+2)²)=√(16+1)=√17
Длина ВС=√((x₂-x₁)² + (y₂-y₁)²)=√((-2+3)² + (4+1)²)=√(1+25)=√26
Значит периметр Р=2·(√17+√26)
г) Составим уравнение прямой АВ по двум точкам:
(x-x₁)/(x₂-x₁)=(y-y₁)/(y₂-y₁)
(x-1)/(-3-1)=(y+2)/(-1+2)
(x-1)/(-4)=(y+2)/1
x-1=-4y-8
x+4y+7=0 (уравнение прямой АВ)