Задача:
Длина окружности, вписанной в правильный треугольник, равна 12π см. Найдите периметр треугольника.
Чтобы найти периметр правильного Δ, нужно знать сторону; что найти сторону, нужно найти радиус вписанной окружности.
Дня нахождения радиуса окружности, воспользуемся формулой длины окружности и выразим из нее радиус:
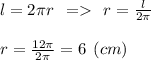
Теперь воспользуемся формулой радиуса вписанной окружности в правильный треугольник для нахождения стороны Δ:
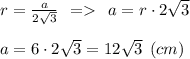
Осталось за малым — периметр правильного треугольника:
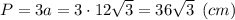
Периметр треугольника равен 36√3 см.
32дм²
Объяснение:
Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S = 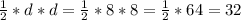 (дм²)
(дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
x² + x² = 8²
2x² = 64
x² = 32
x = √32 = √16*2 = 4√2 (дм)
Площадь квадрата x², то есть площадь равна 32дм²