Профессорская задачка :)
1. Вс задача. В произвольном треугольнике две прямые, выходящие из разных вершин, делятся в точке пересечения в отношении 2:1 и 1:1. Нужно найти, в каком отношении они делят стороны. На самом деле, для заданной задачи достаточно найти, в каком отношении делится сторона, к которой проведена та прямая, которая длится в отношении 2:1. На первом рисунке - простое решение этой задачи. (Не надо путать обозначения тут и при решении основной задачи).
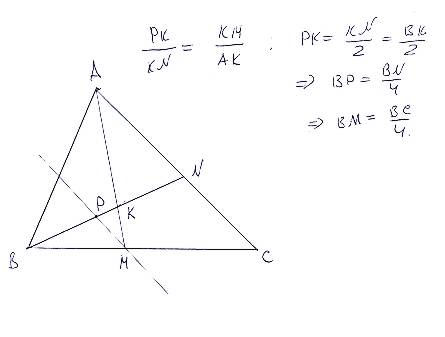
Задано ВК/KN = 1; AK/KM = 2; надо найти BM/BC.
Проводится PM II AC, треугольники PKM и AKN подобны, и PK/KN = KM/AK = 1/2; но КN = BN/2, то есть PN = BN/4; тогда и BP = BN/4; а отсюда BM = BC/4;
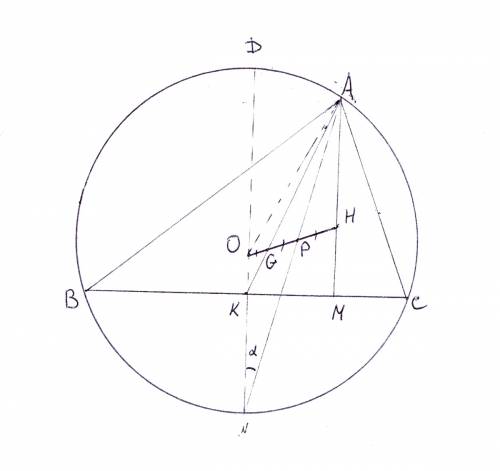
2. Собственно решение. Я изменил обозначение точки пересечения медиан трегольника АВС на букву G. O - центр описанной окружности, Н - ортоцентр. Точка Р пересечения биссектрисы угла А и GН делит GН пополам.
Поскольку АР - биссектриса угла А, то её точка пересечения с окружностью N делит дугу ВС пополам, то есть совпадает с точкой пересечения перпендикуляра к ВС из центра О.
Легко увидеть, что угол DNA между биссектрисой и этим диаметром, обозначенный как α, равен (угол АСВ - угол АВС)/2 (проще всего это понять, если провести через А хорду АА1 II ВС, тогда дуга ВА1 = дуга АС, и угол А1NA = угол А1СА, а DN биссектриса угла A1NA), то есть α = 15°;
Теперь самое главное. Точки O, G и Н лежат на прямой Эйлера, и OG = GH/2; Отсюда следует, что OG = GP = PH; кроме того, точка G делит АК в отношении AG/GK = 2 (ну, это же медиана тр-ка АВС...)
Согласно вс задаче из треугольника AON получается OK = ON/4; то есть расстояние от О до хорды ВС равно четверти радиуса окружности. Отсюда легко найти радиус R описанной окружности. R^2 = 1^2 + (R/4)^2; R = 4/√15;
Для того, чтобы найти площадь, нужно найти АМ. Центральный угол DOA равен 2α = 30°; и равен углу ОАМ, откуда сразу видно, что АМ = ОК + АО*cos(2α) = R*(1/4 + cos(2α)) = R(1/4 + √3/2);
S = ВС*АМ/2 = (4/√15)*(1 + 2√3)/8 = (1 + 2√3)/(2√15);
Я, конечно, мог и ошибиться в арифметике, так что проверяйте, но смысл решения понятен :)
В условии не хватает слов "параллельно АС". В противном случае задача не имеет решения (точнее одного решения, сами по себе решения есть, но - не интересные :) одно из них - треугольник MBD).
Пусть b=8; a = 4; О - центр основания, МО - высота пирамиды, сечение пересекает MD в точке Q (MQ = QD), МС в точке Р, MA - в точке G, МО в точке К. Надо найти площадь четырехугольника BGQP.
Плоскость сечения II АС, поэтому GP II AC, откуда MG/GA = МК/КО = MP/PC = 2/1; поскольку BQ и MO - медианы, и К - точка пересечения медиан треугольника MBD.
то есть
GP = (2/3)*AC = a*2√2/3; (из подобия треугольников AMC и GMP)
И еще, поскольку у квадрата диагонали перпендикулярны, AC перпендикулярно плоскости треугольника MDB, откуда следует, что GP перпендикулярно BQ, то есть площадь S четырехугольника BGQP равна S = BQ*GP/2;
Остается найти медиану m = BQ равнобедренно треугольника MDB с боковыми сторонами MD = MB = b = 8; и основанием BD = a√2; (a = 4);
(2*m)^2 = 2(a√2)^2 + b^2;
m = (1/2)*√(4*a^2 + b^2);
S = (1/2)*(a*2√2/3)*(1/2)*√(4*a^2 + b^2) = (1/6)*a*√(8*a^2 + 2*b^2);
ну и надо подставить числа.
если b = 2*a, то S = (2/3)*a^2 = 32/3;
27.04.2015
Мне предложили тут что-то изменить. Якобы ответ должен быть в 2 раза меньше. Я очень буду рад, если мне предложат грамотный анализ решения. Но я могу показать на пальцах, что ответ верный. Это как раз очень просто. В сечении получается дельтоид, у которого одна из диагоналей BQ = BD; а вторая - GP = (2/3)*AC; отсюда мгновенно понятно, что площадь сечения составляет 2/3 площади основания.
(площадь сечения) = BQ*GP/2 = (2/3)*BD*AC/2 = (2/3)*(площади основания) = (2/3)*4^2 = = 2*16/3 = 32/3;
любые попытки найти тут ошибку могут вызвать только улыбку :
х+40 - величина большего числа.
х+х+40=180
2х+40=180
2х=140
х=70
х+40=70+40=110
ответ. Больший угол равен 110.